题目内容
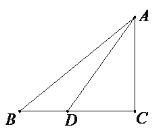
【题目】如图,小明在家乡的楼顶上![]() 处测得池塘的一端
处测得池塘的一端![]() 处的俯角为
处的俯角为![]() ,测得池塘
,测得池塘![]() 处的俯角
处的俯角![]() ,
,![]() 、
、![]() 、
、![]() 三点在同一水平直线上.已知楼高
三点在同一水平直线上.已知楼高![]() 米,求池塘宽
米,求池塘宽![]() 为多少米?(参考数据:
为多少米?(参考数据:![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() .结果保留一位小数.)
.结果保留一位小数.)

【答案】![]() 米
米
【解析】
在Rt△ABC中,tan∠BAC=![]() ,由三角函数得出BC=85.05米,在Rt△ACD中,由三角函数得出CD=AC×tan30
,由三角函数得出BC=85.05米,在Rt△ACD中,由三角函数得出CD=AC×tan30![]() =15×
=15×![]() =5
=5![]() ≈8.65米,即可得出答案.
≈8.65米,即可得出答案.
∵∠BAE=10![]() ,
,
∴∠BAC=90°10°=80°,
在Rt△ABC中,tan∠BAC=![]() ,
,
∴BC=AC×tan80°≈15×5.67=85.05米,
在Rt△ACD中,∠CAD=90°∠EAD=30°,tan∠CAD=![]() ,
,
∴CD=AC×tan30°=15×![]() =5
=5![]() ≈8.65米,
≈8.65米,
∴BD=BCCD=85.058.65≈76.4(米);
答:池塘宽BD约为76.4米.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
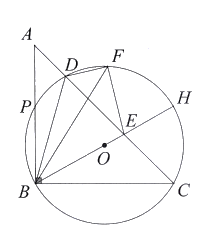
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
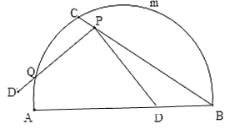
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
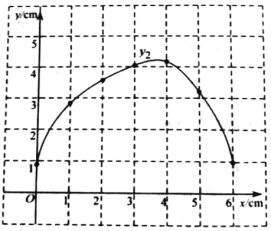
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)