��Ŀ����
����Ŀ����ͼ,�ڱ߳�Ϊ4��������ABCD��,��P��AB�ϴ�A��B�˶�,����DP��AC�ڵ�Q��

��1����֤�������۵�P�˶���AB�Ϻδ�ʱ,������ADQ�ա�ABQ��
��2������P��AB���˶���ʲôλ��ʱ,��ADQ�������������ABCD�����![]() ��
��
��3������P�ӵ�A�˶�����B,�ټ�����BC���˶�����C,�������˶�������,����P�˶���ʲôλ��ʱ,��ADQǡΪ���������Σ�
���𰸡���1��֤������������2��AP=2����3��P��B�㣬C�㣬����CP=4��![]() -1��������ADQ�ǵ��������Σ�
-1��������ADQ�ǵ��������Σ�
��������
�����������1������SAS�����ADQ�ա�ABQ��
��2������Q��QE��AD��E��QF��AB��F����QE=QF������ADQ�������������ABCD�����![]() ������S��ADQ=
������S��ADQ=![]() ADQE=
ADQE=![]() S������ABCD�����OE��ֵ����������DEQ�ס�DAP��
S������ABCD�����OE��ֵ����������DEQ�ס�DAP��![]() �����APֵ��
�����APֵ��
��3����P�˶�ʱ����ADQǡΪ���������ε���������֣���QD=QA��DA=DQ��AQ=AD���������ε�����֪��������P�˶������B�غ�ʱ��QD=QA����ʱ��ADQ�ǵ��������Σ�������P���C�غ�ʱ����Q���CҲ�غϣ���ʱDA=DQ����ADQ�ǵ��������Σ�����AD=AQ=4ʱ����CP=CQ��CP=AC-AD���������εĶԽ��ߵ����ʵõ�CP��ֵ��
�����������1����������ABCD��
���۵�P�˶���AB�Ϻδ�ʱ������
AD=AB����DAQ=��BAQ��AQ=AQ��
���ADQ�ա�ABQ��
��2����ADQ�����ǡ����������ABCD�����![]() ʱ��
ʱ��
����Q��QE��AD��E��QF��AB��F����QE=QF��

���ڱ߳�Ϊ4��������ABCD�У�
��S������ABCD=16��
��![]() AD��QE=
AD��QE=![]() S������ABCD=
S������ABCD=![]() ��16=
��16=![]() ��
��
��QE=![]() ��
��
��EQ��AP��
���DEQ�ס�DAP��
��![]() ����
����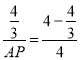 ��
��
���AP=2��
��AP=2ʱ����ADQ�������������ABCD�����![]() ��
��
��3������ADQ�ǵ��������Σ�����QD=QA��DA=DQ��AQ=AD��
����AD=DQʱ������DQA=��DAQ=45��
���ADQ=90����PΪC�㣬
����AQ=DQʱ������DAQ=��ADQ=45����
���AQD=90����PΪB��
��AD=AQ��P��BC�ϣ���
��CQ=AC-AQ=![]() BC-BC=��
BC-BC=��![]() -1��BC
-1��BC
��AD��BC
��![]() �����ɵ�
�����ɵ�![]() =1��
=1��
��CP=CQ=��![]() -1��BC=4��
-1��BC=4��![]() -1��
-1��
���ϣ�P��B�㣬C�㣬����CP=4��![]() -1��������ADQ�ǵ��������Σ�
-1��������ADQ�ǵ��������Σ�

 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�