题目内容
【题目】如图,在平面直角坐标系中,O为坐标原点,已知直线![]() 与x轴、y轴分别交于A、B两点
与x轴、y轴分别交于A、B两点![]() 直线
直线![]() 直线AB于点
直线AB于点![]() 现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止
现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止![]() 设运动时间为t秒.
设运动时间为t秒.![]() 点A的坐标为______;线段OD的长为______.
点A的坐标为______;线段OD的长为______.![]() 设
设![]() 的面积为S,求S与t之间的函数关系
的面积为S,求S与t之间的函数关系![]() 不要求写出取值范围
不要求写出取值范围![]() ,并确定t为何值时S的值最大?
,并确定t为何值时S的值最大?![]() 是否存在某一时刻t,使得
是否存在某一时刻t,使得![]() 为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.
为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.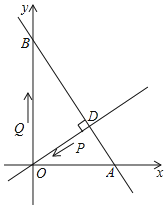
【答案】 ![]()
![]()
【解析】分析:![]() 先求出点B的坐标和A的坐标,进而得出
先求出点B的坐标和A的坐标,进而得出![]() ,利用勾股定理求出AB,利用等面积法即可得出结论;
,利用勾股定理求出AB,利用等面积法即可得出结论;
![]() 先求出
先求出![]() ,进而表示出PH,利用三角形面积公式即可得出结论;
,进而表示出PH,利用三角形面积公式即可得出结论;
![]() 分三种情况利用等腰三角形的性质建立方程即可得出结论.
分三种情况利用等腰三角形的性质建立方程即可得出结论.
详解:![]() 与x轴、y轴分别交于A、B两点,
与x轴、y轴分别交于A、B两点,
令![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案为![]() ;
;
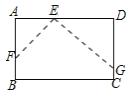
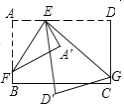
![]() 如图1,
如图1,

在![]() 中,
中,![]() ,
,
根据勾股定理得,![]() ,
,
![]() ,
,
由运动知,![]() ,
,
![]() ,
,
过点P作![]() 于H,
于H,
在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]()
![]() 时,S最大,最大值为
时,S最大,最大值为![]() ;
;
![]() 为等腰三角形,
为等腰三角形,
![]() 当
当![]() 时,
时,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,在
时,在![]() 中,
中,![]() ,
,
如图2,过点Q作![]() 于M,
于M,

![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,如图3,
时,如图3,

过点P作![]() 于H,
于H,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等腰三角形时,t的值为
为等腰三角形时,t的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒
秒![]()

练习册系列答案
相关题目
【题目】下表记录了一名球员在罚球线上投篮的结果.
投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率( |
|
|
|
|
|
|
|
(1)计算表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?