��Ŀ����
����Ŀ��̽�����⣺
(1)��������
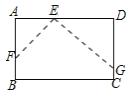
��ͼ�٣���������ABCD�У���E��F�ֱ�ΪDC��BC���ϵĵ㣬�������BAF��45�㣬����EF����֤DE��BF��EF��������ⷽ���������������գ�����ADE�Ƶ�A˳ʱ����ת90��õ���ABG����ʱAB��AD�غϣ�����ת�ɵã�AB��AD��BG��DE����1����2����ABG����D��90�㣬�� ��ABG����ABF��90�㣫90�㣽180�㣬��ˣ���G��B��F��ͬһ��ֱ���ϣ�
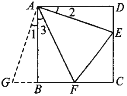
�� ��EAF��45��� ��2����3����BAD����EAF��90�㣭45�㣽45�㣮
�� ��1����2����1����3��45�㣮
����GAF����________��
��AG��AE��AF��AE
�� ��GAF�ա�________��
�� _________��EF����DE��BF��EF��
(2)����Ǩ�ƣ�
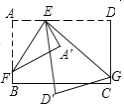
��ͼ�ڣ���Rt��ABC��б�߷��۵õ���ADC����E��F�ֱ�ΪDC��BC���ϵĵ㣬�ҡ�EAF��![]() ��DAB���Բ���DE��BF��EF֮���к�������ϵ����֤����IJ��룮
��DAB���Բ���DE��BF��EF֮���к�������ϵ����֤����IJ��룮
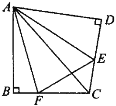
���𰸡�(1)EAF����EAF��GF��(2)DE��BF��EF.
��������
��1�����ý�֮��ĵ��������ó���GAF=��FAE��������SAS�ó���GAF�ա�EAF���ó��𰸣�
��2������ADE˳ʱ����ת90���õ���ABG����֤����AGF�ա�AEF�����ɵó��𰸣�
�⣺��1����ͼ����ʾ��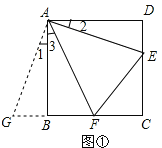
���ݵ��������ó���GAF=��FAE��
����SAS�ó���GAF�ա�EAF��
��GF=EF��
�ʴ�Ϊ��FAE����EAF��GF��
(2)DE��BF��EF���������£�
������BAD�Ķ���Ϊm������ADE�Ƶ�A˳ʱ����ת��m���õ���ABG����ͼ����ʱAB��AD�غϣ�����ת�ɵã�
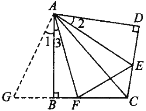
AB��AD��BG��DE����1����2����ABG����D��90����
�� ��ABG����ABF��90����90����180����
��ˣ���G��B��F��ͬһ��ֱ���ϣ�
�� ![]() ��
��
�� ![]() ��
��
�� ��1����2��
�� ��1����3��![]() ��
��
����GAF����EAF��
������AGF����AEF��
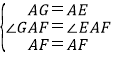 ��
��
�� ��GAF�ա�EAF��SAS����
�� GF��EF��
���� GF��BG��BF��DE��BF��
�� DE��BF��EF��

����Ŀ���±���¼��һ����Ա�ڷ�������Ͷ���Ľ����
Ͷ������(n) | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
Ͷ�д���(m) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
Ͷ��Ƶ��( | �� | �� | �� | �� | �� | �� | �� |
(1)������е�Ͷ��Ƶ��(��ȷ��0.01)��
(2)������ԱͶ��һ�Σ�Ͷ�еĸ���Լ�Ƕ���(��ȷ��0.1)��