题目内容
如图9所示, 是边长为
是边长为 的等边三角形,其中
的等边三角形,其中 是坐标原点,顶点
是坐标原点,顶点 在
在 轴的正方向上,将
轴的正方向上,将 折叠,使点
折叠,使点 落在边
落在边 上,记为
上,记为 ,折痕为
,折痕为 。
。
小题1:设 的长为
的长为 ,
, 的周长为
的周长为 ,求
,求 关于
关于 的函数关系式.
的函数关系式.
小题2:当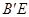 //y轴时,求点
//y轴时,求点 和点
和点 的坐标.
的坐标.
小题3:当 在
在 上运动但不与
上运动但不与 、
、 重合时,能否使
重合时,能否使 成为直角三角形?若能,请求出点
成为直角三角形?若能,请求出点 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
 \
\
 是边长为
是边长为 的等边三角形,其中
的等边三角形,其中 是坐标原点,顶点
是坐标原点,顶点 在
在 轴的正方向上,将
轴的正方向上,将 折叠,使点
折叠,使点 落在边
落在边 上,记为
上,记为 ,折痕为
,折痕为 。
。小题1:设
 的长为
的长为 ,
, 的周长为
的周长为 ,求
,求 关于
关于 的函数关系式.
的函数关系式.小题2:当
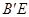 //y轴时,求点
//y轴时,求点 和点
和点 的坐标.
的坐标.小题3:当
 在
在 上运动但不与
上运动但不与 、
、 重合时,能否使
重合时,能否使 成为直角三角形?若能,请求出点
成为直角三角形?若能,请求出点 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由. \
\小题1:解:∵
 和B关于EF对称,∴
和B关于EF对称,∴ E=BE,
E=BE,∴
 =
= =
= =
= .
.小题2:解:当
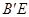 //y轴时,∠
//y轴时,∠ =90°。
=90°。∵△OAB为等边三角形,∴∠EO
 =60°,O
=60°,O =
= EO。
EO。设
 ,则OE=
,则OE= 。
。 在Rt△OE
 中,tan∠EO
中,tan∠EO =
= ,
,∴
 E=
E= Otan∠EO
Otan∠EO =
=
∵
 E+ OE=BE+OE=2+
E+ OE=BE+OE=2+ ,∴
,∴ ,
,∴
 (1,0),E(1,
(1,0),E(1, )。
)。小题3:答:不能。
理由如下:∵∠E
 F=∠B=60°,
F=∠B=60°,∴要使△E
 F成为直角三角形,则90°角只能是∠
F成为直角三角形,则90°角只能是∠ EF或
EF或∠
 FE。 假设∠
FE。 假设∠ EF=90°,
EF=90°,∵△F
 E与△FBE关于FE对称,
E与△FBE关于FE对称,∴∠BEF=∠
 EF=90°,
EF=90°,∴∠BE
 =180°,
=180°,则
 、E、B三点在同一直线上,
、E、B三点在同一直线上, 与O重合。
与O重合。这与题设矛盾。
∴∠
 EF≠90°。
EF≠90°。即△E
 F不能为直角三角形。
F不能为直角三角形。同理,∠
 FE=90°也不成立。
FE=90°也不成立。∴△E
 F不能成为直角三角形。
F不能成为直角三角形。略

练习册系列答案
相关题目
 ,0)绕着原点顺时针方向旋转60°得到点 B,则点B的坐标是 ▲ .
,0)绕着原点顺时针方向旋转60°得到点 B,则点B的坐标是 ▲ .
 平面直角坐标系中,已知,ΔABO的三个顶点的坐标分别为A(2,2),B(0,4),O(0,0);
平面直角坐标系中,已知,ΔABO的三个顶点的坐标分别为A(2,2),B(0,4),O(0,0);  0并写出点A
0并写出点A ,B
,B
 程中两三角板的重叠部分(如图②).
程中两三角板的重叠部分(如图②).
 ?若存在,求出此时BH的长度;若不存在,说明理由.
?若存在,求出此时BH的长度;若不存在,说明理由. 


 ;
;