题目内容
下列图形中,既是中心对称图形又是轴对称图形的是

B
第一个是轴对称图形,不是中心对称图形;
第二个是轴对称图形,也是中心对称图形;
第三个不是轴对称图形,是中心对称图形;
第四个不是轴对称图形,也不是中心对称图形.
故选B.
第二个是轴对称图形,也是中心对称图形;
第三个不是轴对称图形,是中心对称图形;
第四个不是轴对称图形,也不是中心对称图形.
故选B.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
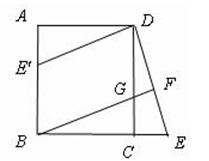
 OB长为半径作⊙O,若射线BA绕点B按顺时针方向旋转至
OB长为半径作⊙O,若射线BA绕点B按顺时针方向旋转至 ,若
,若 (0° <
(0° <
 三个顶点的坐标分别为
三个顶点的坐标分别为 
 顺时针旋转
顺时针旋转 后得到的
后得到的 ,并求出
,并求出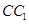 的长.
的长.
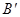 位置,A点落在
位置,A点落在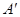 位置,若
位置,若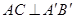 ,则
,则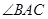 的度数是 .
的度数是 .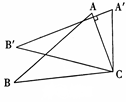
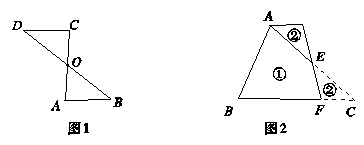

 是边长为
是边长为 的等边三角形,其中
的等边三角形,其中 是坐标原点,顶点
是坐标原点,顶点 在
在 轴的正方向上,将
轴的正方向上,将 落在边
落在边 上,记为
上,记为 ,折痕为
,折痕为 。
。 的长为
的长为 的周长为
的周长为 ,求
,求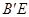 //y轴时,求点
//y轴时,求点 的坐标.
的坐标. 成为直角三角形?若能,请求出点
成为直角三角形?若能,请求出点 \
\
