题目内容
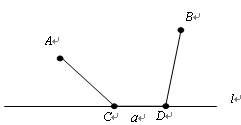
(本题满分8分)如图,将长方形纸片的两角分别折叠,使顶点B落在B′处,顶点A落在A′处,EC、ED为折痕,并且点E、A′、B′在同一条直线上。若∠BED=320,求∠CED和∠AEC的度数。
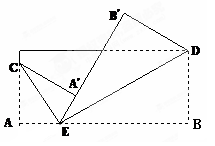

解:∠CED =900, ┉┉4分
∠AEC =580┉┉8分
分析:根据翻折的性质,只要证明∠2+∠3=90°即可;根据∠2+∠3=90°及对角线知识可求得∠AEC。
解答:
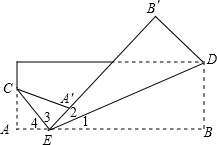
∵EC和ED是折痕,
∴∠1=∠2,∠3=∠4,
又∵∠1+∠2+∠3+∠4=180°,
∴2(∠2+∠3)=180°,
∴∠2+∠3=90°,
即∠CED=90°。
又∠2=∠1=32°,
∴∠4=∠3=90°-∠1=90°-32°=58°,
即∠AEC=58°。
点评:本题考查翻折变换的知识,折叠问题要重视折痕,找清折痕两边重合的部分,即相等的边,相等的角有哪些,找准这些关系对解决题目有很大帮助。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
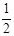 OB长为半径作⊙O,若射线BA绕点B按顺时针方向旋转至
OB长为半径作⊙O,若射线BA绕点B按顺时针方向旋转至 ,若
,若 (0° <
(0° <
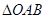 是边长为
是边长为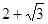 的等边三角形,其中
的等边三角形,其中 是坐标原点,顶点
是坐标原点,顶点 在
在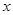 轴的正方向上,将
轴的正方向上,将 落在边
落在边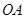 上,记为
上,记为 ,折痕为
,折痕为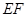 。
。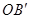 的长为
的长为 的周长为
的周长为 ,求
,求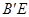 //y轴时,求点
//y轴时,求点 的坐标.
的坐标. 成为直角三角形?若能,请求出点
成为直角三角形?若能,请求出点 \
\
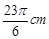
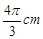

 (5,
(5,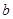 )与点
)与点 (
(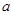 ,-3)关于y轴对称,则
,-3)关于y轴对称,则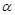 角(
角( ),当点A的对应点与点C重合时,B,C两点的对应点分别记为E,F,EF与AB的交点为G,此时
),当点A的对应点与点C重合时,B,C两点的对应点分别记为E,F,EF与AB的交点为G,此时
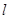 同侧,在直线
同侧,在直线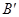 ,连接
,连接 ,与直线
,与直线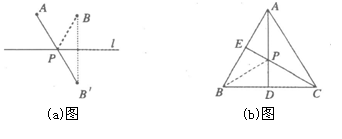
 ),使得AC+CD+DB最短.(不要求写画法)
),使得AC+CD+DB最短.(不要求写画法)