题目内容
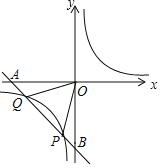
【题目】如图,已知反比例函数y=![]() (m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).
(m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).
(1)求反比例函数与一次函数的表达式;
(2)一次函数的图象分别与x轴、y轴交于A、B两点,与反比例函数图象的另一个交点为P点,连结OP、OQ,求△OPQ的面积.
【答案】(1)反比例函数的表达式为![]() ,一次函数的表达式y=﹣x﹣5;(2)7.5.
,一次函数的表达式y=﹣x﹣5;(2)7.5.
【解析】(1)根据待定系数法,将点的坐标分别代入两个函数的表达式中求出待定系数,可得答案;
(2)利用△AOP的面积减去△AOQ的面积.
(1)反比例函数y=![]() ( m≠0)的图象经过点(1,4),
( m≠0)的图象经过点(1,4),
∴4=![]() ,解得m=4,故反比例函数的表达式为y=
,解得m=4,故反比例函数的表达式为y=![]() ,
,
一次函数y=-x+b的图象与反比例函数的图象相交于点Q(-4,n),
∴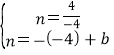 ,解得
,解得![]() ,
,
∴一次函数的表达式y=-x-5;
(2)由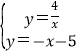 ,解得
,解得![]() 或
或![]() ,
,
∴点P(-1,-4),
在一次函数y=-x-5中,令y=0,得-x-5=0,解得x=-5,故点A(-5,0),
S△OPQ=S△OPA-S△OAQ=![]() ×5×4
×5×4![]() ×5×1=7.5.
×5×1=7.5.

 阅读快车系列答案
阅读快车系列答案【题目】北京地铁1号线(BeijingSubwayLine1),是中国第一条地铁线路,1969年10月1日,第一辆地铁机车从古城站呼啸驶出.北京地铁一期工程赶在新中国成立20周年的时侯建成通车了,宣告了中国没有地铁历史的结束.
下图是北京1号线地铁部分相邻站间距信息统计表.
1号线部分相邻站间距信息统计表 | ||
起始/终到车站 | 区间距离(单位:km) | 近似区间距离(精确到个位) |
玉泉路﹣﹣八宝山 | 1.479 |
|
八宝山﹣﹣八角游乐园 | 1.953 |
|
八角游乐园﹣﹣古城 | 1.921 |
|
古城﹣﹣苹果园 | 2.606 |
|
(1)请你填写上表,并利用近似区间距离,选取适当的参照物,借助数轴,尽可能清晰地描绘出上述5个站点的位置;
(2)有如下四个结论:
①当表示八角游乐园的点所表示的数为0,表示八宝山的点所表示的数为﹣2时,表示古城的点所表示的数为2;
②当表示八角游乐园的点所表示的数为0,表示八宝山的点所表示的数为﹣4时,表示古城的点所表示的数为4;
③当表示八角游乐园的点所表示的数为1,表示八宝山的点所表示的数为﹣3时,表示古城的点所表示的数为5;
④当表示八角游乐园的点所表示的数为﹣1,表示八宝山的点所表示的数为﹣5时,表示古城的点所表示的数为3.
上述结论中,所有正确结论的序号是 .