Question

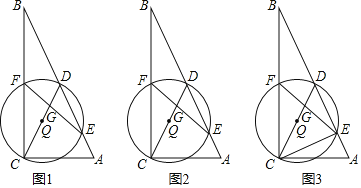
【题目】已知：在Rt△ABC中，∠ACB＝90°，AC＝1，D是AB的中点，以CD为直径的⊙Q分别交BC、BA于点F、E，点E位于点D下方，连接EF交CD于点G．

（1）如图1，如果BC＝2，求DE的长；

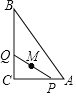
（2）如图2，设BC＝x，＝y，求y关于x的函数关系式及其定义域；

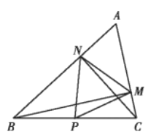
（3）如图3，连接CE，如果CG＝CE，求BC的长．

Answer 1

【答案】（1）DE＝；（2）y＝（x＞1）．（3）BC＝1+．

【解析】

（1）如图1中，连接CE．在Rt△CDE中，求出CD，CE即可解决问题．

（2）如图2中，连接CE，设AC交⊙Q于K，连接FK，DF，DK．想办法用x表示CD，DE，证明FK∥AB，推出，延长构建关系式即可解决问题．根据点E位于点D下方，确定x的取值范围即可．

（3）如图3中，连接FK．证明ED＝EC，由此构建方程即可解决问题．

（1）如图1中，连接CE．

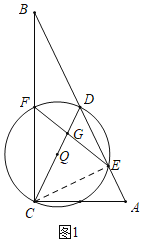
在Rt△ACB中，∵∠ACB＝90°，AC＝1，BC＝2，

∴AB＝，

∵CD 是⊙Q的直径，

∴∠CED＝90°，

∴CE⊥AB，

∵BD＝AD，

∴CD＝

∵ABCE＝BCAC，

∴CE＝，

在Rt△CDE中，DE＝．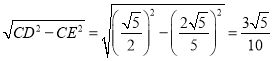

（2）如图2中，连接CE，设AC交⊙Q于K，连接FK，DF，DK．

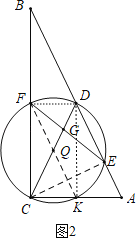
∵∠FCK＝90°，

∴FK是⊙Q的直径，

∴直线FK经过点Q，

∵CD是⊙Q的直径，

∴∠CFD＝∠CKD＝90°，

∴DF⊥BC，DK⊥AC，

∵DC＝DB＝DA，

∴BF＝CF，CK＝AK，

∴FK∥AB，

∴，

∵BC＝x，AC＝1，

∴AB＝，

∴DC＝DB＝DA＝，

∵△ACE∽△ABC，

∴可得AE＝，

∴DE＝AD﹣AE＝，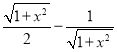

∴，

，

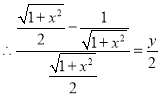∴y＝（x＞1）．

（3）如图3中，连接FK．

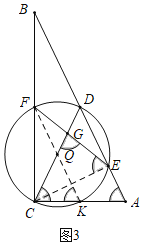
∵CE＝CG，

∴∠CEG＝∠CGE，

∵∠FKC＝∠CEG，

∵FK∥AB，

∴∠FKC＝∠A，

∵DC＝DA，

∴∠A＝∠DCA，

∴∠A＝∠DCA＝∠CEG＝∠CGE，

∴∠CDA＝∠ECG，

∴EC＝DE，

由（2）可知：，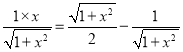

整理得：x2﹣2x﹣1＝0，

∴x＝1+或1﹣（舍弃），

∴BC＝1+．