Question

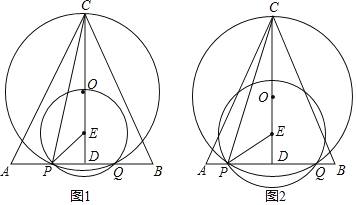
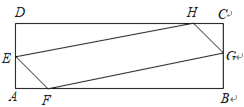
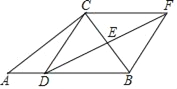
【题目】如图，在△ABC中，D是AB边上任意一点，E是BC边中点，过点C作AB的平行线，交DE的延长线于点F，连接BF，CD．

（1）求证：四边形CDBF是平行四边形；

（2）若∠FDB=30°，∠ABC=45°，BC=4，求DF的长．

Answer 1

【答案】（1）证明见解析；（2）8.

【解析】

（1）先证明出△CEF≌△BED，得出CF=BD即可证明四边形CDBF是平行四边形；

（2）作EM⊥DB于点M，根据平行四边形的性质求出BE，DF的值，再根据三角函数值求出EM的值，∠EDM=30°，由此可得出结论．

（1）证明：∵CF∥AB，

∴∠ECF=∠EBD．

∵E是BC中点，

∴CE=BE．

∵∠CEF=∠BED，

∴△CEF≌△BED．

∴CF=BD．

∴四边形CDBF是平行四边形．

（2）解：如图，作EM⊥DB于点M，

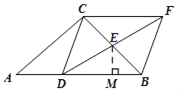
∵四边形CDBF是平行四边形，BC=，

∴，DF=2DE．

在Rt△EMB中，EM=BEsin∠ABC=2，

在Rt△EMD中，∵∠EDM=30°，

∴DE=2EM=4，

∴DF=2DE=8．