题目内容
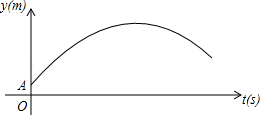
【题目】如图,某足球运动员站在点O处练习射门.将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,己知足球飞行0.8s时,离地面的高度为3.5m.
(1)a= ,c= ;
(2)当足球飞行的时间为多少时,足球离地面最高?最大高度是多少?
(3)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
【答案】(1)![]() ,
,![]() ;(2)当足球飞行的时间
;(2)当足球飞行的时间![]() s时,足球离地面最高,最大高度是4.5m;(3)能.
s时,足球离地面最高,最大高度是4.5m;(3)能.
【解析】
(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),代入函数的表达式即可求出a,c的值;
(2)利用配方法即可求出足球飞行的时间以及足球离地面的最大高度;
(3)把x=28代入x=10t得t=2.8,把t=2.8代入解析式求出y的值和2.44m比较大小即可得到结论.
(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴![]() ,
,
解得: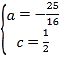 ,
,
∴抛物线的解析式为:y=﹣![]() t2+5t+
t2+5t+![]() ,
,
故答案为:﹣![]() ,
,![]() ;
;
(2)∵y=﹣![]() t2+5t+
t2+5t+![]() ,
,
∴y=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,y最大=4.5,
时,y最大=4.5,
∴当足球飞行的时间![]() s时,足球离地面最高,最大高度是4.5m;
s时,足球离地面最高,最大高度是4.5m;
(3)把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=﹣![]() ×2.82+5×2.8+
×2.82+5×2.8+![]() =2.25<2.44,
=2.25<2.44,
∴他能将球直接射入球门.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目