题目内容
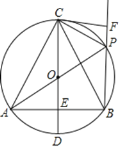
【题目】如图，在⊙O中，点C为
的中点，∠ACB＝120°，OC的延长线与AD交于点D，且∠D＝∠B．
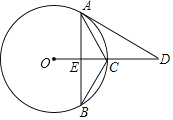
（1）求证：AD与⊙O相切；
（2）若CE＝4，求弦AB的长．
【答案】（1）见解析；（2）8
【解析】
（1）连接OA，由
，得CA=CB，根据题意可得出∠O=60°，从而得出∠OAD=90°，则AD与⊙O相切；
（2）由题意得OC⊥AB，Rt△BCE中，由三角函数得BE=4，即可得出AB的长．
（1）证明：如图，连接OA，
∵，
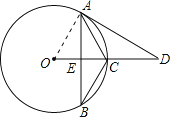
∴CA＝CB，
又∵∠ACB＝120°，
∴∠B＝30°，
∴∠O＝2∠B＝60°，
∵∠D＝∠B＝30°，
∴∠OAD＝180°﹣（∠O+∠D）＝90°，
∴AD与⊙O相切；
（2）∵∠O＝60°，OA＝OC，
∴△OAC是等边三角形，
∴∠ACO＝60°，
∵∠ACB＝120°，
∴∠ACB＝2∠ACO，AC＝BC，
∴OC⊥AB，AB＝2BE，
∵CE＝4，∠B＝30°，
∴BC＝2CE＝8，
∴BE＝
＝
＝4，
∴AB＝2BE＝8，
∴弦AB的长为8．
【题目】农经公司以30元/千克的价格收购一批农产品进行销售，为了得到日销售量p（千克）与销售价格x（元/千克）之间的关系，经过市场调查获得部分数据如下表：
销售价格x（元/千克） | 30 | 35 | 40 | 45 | 50 |
日销售量p（千克） | 600 | 450 | 300 | 150 | 0 |
（1）请你根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式；
（2）农经公司应该如何确定这批农产品的销售价格，才能使日销售利润最大？
（3）若农经公司每销售1千克这种农产品需支出a元（a＞0）的相关费用，当40≤x≤45时，农经公司的日获利的最大值为2430元，求a的值．（日获利=日销售利润﹣日支出费用）
【题目】某公司经销的一种产品每件成本为40元，要求在90天内完成销售任务．已知该产品90天内每天的销售价格与时间（第x天）的关系如下表：
时间（第x天） | 1≤x＜50 | 50≤x≤90 |
x+50 | 90 |
任务完成后，统计发现销售员小王90天内日销售量p（件）与时间（第x天）满足一次函数关系p＝﹣2x+200．设小王第x天销售利润为W元．
（1）直接写出W与x之间的函数关系式，井注明自变量x的取值范围；
（2）求小生第几天的销售量最大？最大利润是多少？
（3）任务完成后，统计发现平均每个销售员每天销售利润为4800公司制定如下奖励制度：如果一个销售员某天的销售利润超过该平均值，则该销售员当天可获得200元奖金．请计算小王一共可获得多少元奖金？
