题目内容
【题目】如图,在平面直角坐标系中,点A(0,4)、B(﹣3,0),将线段AB沿x轴正方向平移n个单位得到菱形ABCD.
(1)画出菱形ABCD,并直接写出n的值及点D的坐标;
(2)已知反比例函数y=![]() 的图象经过点D,ABMN的顶点M在y轴上,N在y=
的图象经过点D,ABMN的顶点M在y轴上,N在y=![]() 的图象上,求点M的坐标;
的图象上,求点M的坐标;
(3)若点A、C、D到某直线l的距离都相等,直接写出满足条件的直线解析式.

【答案】(1)n=5,点D坐标为(5,4);(2)M(0,![]() );(3)y=﹣2x+9.
);(3)y=﹣2x+9.
【解析】
(1)由勾股定理和菱形的性质可得AB=BC=CD=AD=5,即可求n的值及点D的坐标;
(2)过点N作NH⊥OA于点H,由平行四边形的性质可得AN=BM,AN∥BM,可得∠BMO=∠NAH,由“AAS”可证△ANH≌△MBO,可得HN=BO=3,MO=AH,即可求点M坐标;
(3)由点A、C、D到某直线l的距离都相等,可得直线l是△ACD的中位线所在直线,由待定系数法可求直线解析式.
解:(1)如图,
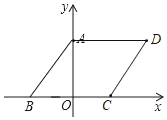
∵点A(0,4)、B(﹣3,0),
∴AO=4,BO=3,
∴AB=![]() =5,
=5,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,
∵将线段AB沿x轴正方向平移n个单位得到菱形ABCD,
∴n=5,点C坐标为(2,0),点D坐标为(5,4);
(2)∵反比例函数y=![]() 的图象经过点D,
的图象经过点D,
∴k=4×5=20,
∵N在y=![]() 的图象上,
的图象上,
∴设点N(a,![]() ),
),
如图,过点N作NH⊥OA于点H,
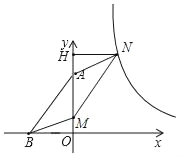
∵四边形ABMN是平行四边形
∴AN=BM,AN∥BM,
∴∠BMA=∠NAM,
∴∠BMO=∠NAH,且AN=BM,∠BOM=∠NHA=90°,
∴△ANH≌△MBO(AAS),
∴HN=BO=3,MO=AH,
∴HN=a=3,HO=![]() ,
,
∴OM=AH=HO﹣AO=![]() ,
,
∴点M(0,![]() );
);
(3)∵点A、C、D到某直线l的距离都相等,
∴直线l是△ACD的中位线所在直线,
如图所示:
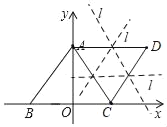
若直线l过线段AC,CD中点,
∴直线l的解析式为:y=2,
若直线l过线段AD,AC中点,即直线l过点(![]() ,4),点(1,2),
,4),点(1,2),
设直线l的解析式为:y=mx+n
∴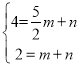 ,
,
解得:m=![]() ,n=
,n=![]() ,
,
∴直线l的解析式为:y=![]() ,
,
若直线l过线段AD,CD中点,即直线l过点(![]() ,4),点(
,4),点(![]() ,2),
,2),
设直线l解析式为:y=kx+b
∴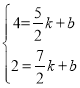 ,
,
解得:k=﹣2,b=9,
∴直线l的解析式为:y=﹣2x+9.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案