Question

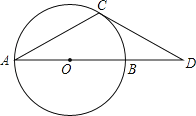
【题目】如图，AB是⊙O的直径，点D在AB的延长线上，点C在⊙O上，CA＝CD，∠CDA＝30°．

（1）试判断直线CD与⊙O的位置关系，并说明理由；

（2）若⊙O的半径为4，

①用尺规作出点A到CD所在直线的距离；

②求出该距离．

Answer 1

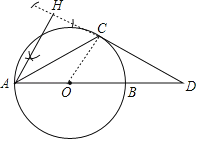
【答案】（1）CD与⊙O相切．理由见解析；（2）①如图，AH为所作；见解析；②点A到CD所在直线的距离为6．

【解析】

（1）连接OC，如图，利用等腰三角形的性质得到∠CAD＝∠CDA＝30°，∠OCA＝∠OAC＝30°，则利用三角形内角和计算出∠OCD＝90°，然后根据切线的判定定理可判断CD为⊙O的切线；

（2）①如图，利用基本作图，过点A作AH⊥CD于H即可；②在Rt△OCD中利用含30度的直角三角形三边的关系得到OD＝8，则AD＝12，从而可求出AH的长．

（1）CD与⊙O相切．

理由如下：连接OC，如图，

∵CA＝CD，

∴∠CAD＝∠CDA＝30°，

∵OA＝OC，

∴∠OCA＝∠OAC＝30°，

∴∠OCD＝180°﹣3×30°＝90°，

∴OC⊥CD，

∴CD为⊙O的切线；

（2）①如图，AH为所作；

②在Rt△OCD中，∵∠D＝30°，

∴OD＝2OC＝8，

∴AD＝8+4＝12，

在Rt△ADH中，AH＝AD＝6，

即点A到CD所在直线的距离为6．