题目内容
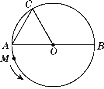
【题目】如图，直线y＝－
x＋3与x轴相交于点A，与y轴相交于点B，点C是第二象限内任意一点，以点C为圆心的圆与x轴相切于点E，与直线AB相切于点F.
(1)如图①，当四边形OBCE是矩形时，求点C的坐标；
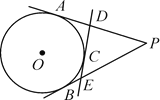
(2)如图②，若⊙C与y轴相切于点D，求⊙C的半径r；
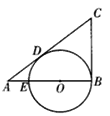
(3)在⊙C的移动过程中，能否使△OEF是等边三角形？(只回答“能”或“不能”)
【答案】（1）点C的坐标为(－5，3)；（2）r＝2；（3）不能．
【解析】
（1）因为直线y
x+3与x轴相交于点A，与y轴相交于点B，所以分别令x=0，y=0，可求出A（4，0），B（0，3），所以OA=4，OB=3，AB=5，连接CF，当四边形OBCE为矩形时，有CF=CE=OB=3，CB∥x轴，利用两直线平行同位角相等可得∠CBF=∠BAO，又因⊙C与直线AB相切于点F，所以CF⊥AB于点F，利用AAS可知△CBF≌△BAO，所以CB=AB=5，即点C的坐标为（﹣5，3）；
（2）因为点C（m，n）是第二象限内任意一点，以点C为圆心的圆与x轴相切于点E，与直线AB相切于点F，若⊙C与y轴相切于点D，可分别连接CE、CF、CD，则由切线长定理得AF=AE，BF=BD，OD=OE，所以AE
（AB+OA+OB）=6，又因由切线性质定理得：CE⊥x轴于点E，CD⊥y轴于点D，所以四边形CEOD为矩形，又因为CE=CD，所以四边形CEOD为正方形，所以OE=CE=r=AE﹣OA=6﹣4=2；
（3）用反证法证明即可．假设△OEF是等边三角形，得到∠FEO=60°．由切线长定理得AF=AE，从而得到△AEF是等边三角形，故有∠EAB=60°．在△OAB中，tan∠OAB=
≠tan60°，产生了矛盾，即三角形OEF不是等边三角形．
（1）如图1，当x=0时，y=3；当y=0时，x=4，∴A（4，0），B（0，3），∴OA=4，OB=3，AB=5．
连接CF，当四边形OBCE为矩形时，有CF=CE=OB=3，CB∥x轴，∴∠CBF=∠BAO
∵⊙C与直线AB相切于点F，∴CF⊥AB于点F
∴∠CFB=∠BOA．
又∵CF=OB，∴△CBF≌△BAO，∴CB=AB=5，∴点C的坐标为（﹣5，3）；
（2）如图2，连接CE、CF、CD．
∵⊙C与x轴、y轴、AB分别相切于E、D、F，∴由切线长定理得AF=AE，BF=BD，OD=OE，∴AE（AB+OA+OB）=6，由切线性质定理得：CE⊥x轴于点E，CD⊥y轴于点D，∴四边形CEOD为矩形．
又∵CE=CD，∴矩形CEOD为正方形，∴OE=CE=r．
∵OE=AE﹣OA=6﹣4=2，∴⊙C的半径为2；
（3）不能．理由如下：
如图3，假设△OEF是等边三角形，∴∠FEO=60°．
∵AF、AE是切线，∴AF=AE，∴△AEF是等边三角形，∴∠EAB=60°．在△OAB中，tan∠OAB=≠tan60°，∴产生了矛盾，即三角形OEF不是等边三角形．
