题目内容
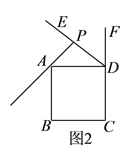
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

【答案】(1)AB⊥EF ∠BAE=90° ∠ABC=∠EAC(2)详见解析
【解析】
(1)根据切线的判断由![]() 或
或![]() 可判断
可判断![]() 为
为![]() 的切线;当
的切线;当![]() ,根据圆周角定理得
,根据圆周角定理得![]() ,所以
,所以![]() ,即
,即![]() ,于是也可判断
,于是也可判断![]() 为
为![]() 的切线;
的切线;
(2)作直径![]() ,连结
,连结![]() ,由
,由![]() 为直径得
为直径得![]() ,则
,则![]() ,根据圆周角定理得
,根据圆周角定理得![]() ,而
,而![]() ,所以
,所以![]() ,则
,则![]() ,根据切线的判定定理得到
,根据切线的判定定理得到![]() 为
为![]() 的切线.
的切线.
(1)当 AB⊥EF 或∠BAE=90°可判断 EF 为⊙O 的切线;
当∠ABC=∠EAC,∵AB 为直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∴∠EAC+∠CAB=90°,
∴AB⊥EF,
∴EF 为⊙O 的切线;
故答案为 AB⊥EF、∠BAE=90°、∠ABC=∠EAC;
(2)证明:作直径 AD,连结 CD,
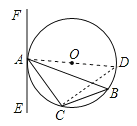
∵AD 为直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴EF 为⊙O 的切线.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目