题目内容
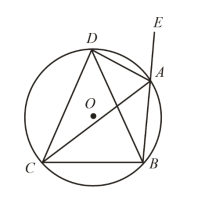
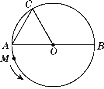
【题目】如图,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.
(1)求∠AOC的度数;
(2)如图,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.
【答案】(1)∠AOC=60°;(2)当S△MAO=S△CAO时,动点M所经过的弧长为![]() π或
π或![]() π或
π或![]() π或
π或![]() π.
π.
【解析】
(1)根据等腰三角形中有一角为60度时是等边三角形得到△ACO是等边三角形,即可得到结论;
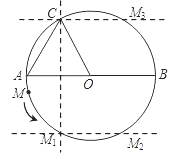
(3)如图,当S△MAO=S△CAO时,动点M的位置有四种.
①作点C关于直径AB的对称点M1,连接AM1,OM1;②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2;③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3;④当点M运动到C时,M与C重合,求得每种情况的OM转过的度数,再根据弧长公式求得弧AM的长.
(1)在△ACO中,∵∠OAC=60°,OC=OA,∴△ACO是等边三角形,∴∠AOC=60°.
(2)如图,分四种情况讨论:
①作点C关于直径AB的对称点M1,连接AM1,OM1.
易得:S△M1AO=S△CAO,∠AOM1=60°,∴![]() ,∴当点M运动到M1时,S△MAO=S△CAO,此时点M经过的弧长为
,∴当点M运动到M1时,S△MAO=S△CAO,此时点M经过的弧长为![]() .
.
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得:![]() =S△CAO,∴∠AOM1=∠M1OM2=∠BOM2=60°,∴
=S△CAO,∴∠AOM1=∠M1OM2=∠BOM2=60°,∴![]() 或
或![]() ,∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为
,∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为![]() .
.
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得:![]() =S△CAO,∴∠BOM3=60°,∴
=S△CAO,∴∠BOM3=60°,∴![]() 或
或![]() ,∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为
,∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为![]() .
.
④当点M运动到C时,M与C重合,S△MAO=S△CAO,此时点M经过的弧长为![]() 或
或![]() .
.
综上所述:当S△MAO=S△CAO时,动点M所经过的弧长为![]() π或
π或![]() π或
π或![]() π或
π或![]() π.
π.

 名校课堂系列答案
名校课堂系列答案