题目内容
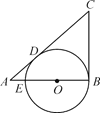
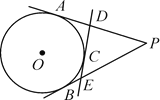
【题目】如图，P是⊙O外一点，PA，PB分别和⊙O切于A，B两点，C是弧AB上任意一点，过点C作⊙O的切线分别交PA，PB于点D，E.若△PDE的周长为12，则PA的长为( )
A. 12 B. 6 C. 8 D. 4
【答案】B
【解析】
由PA，PB分别和⊙O切于A，B两点， DE是⊙O的切线，根据切线长定理，即可得PA=PB，DA=DC，EB=EC，又由△PDE的周长为12，易求得PA+PB=12，则可求得答案．
∵PA，PB分别和⊙O切于A，B两点，
∴PA=PB，
∵DE是O的切线，
∴DA=DC，EB=EC，
∵△PDE的周长为12，
即PD+DE+PE
=PD+DC+EC+PE
=PD+AD+EB+PE
=PA+PB
=2PA
=12，
∴PA=6.
故选B.
练习册系列答案
阅读快车系列答案
相关题目
