题目内容
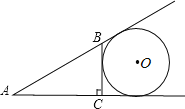
【题目】如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
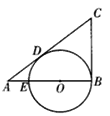
【答案】(1)BE=6;(2) S△ABC=24..
【解析】
(1)连接OD,由切线的性质得OD⊥AC,,在Rt△ODA中运用勾股定理可以求出半径OD,即可求得直径BE的长;
(2)由切线长定理知,CD=BC,在Rt△ABC中运用勾股定理可以求出BC,则可由直角三角形的面积公式求得△ABC的面积.
(1)连接OD,

∴OD⊥AC
∴△ODA是直角三角形
设半径为r
∴AO=r+2
∴![]()
解之得:r=3
∴BE=6
(2)∵∠ABC=900
∴OB⊥BC
∴BC是⊙O的切线
∵CD切⊙O于D
∴CB=CD
令CB=x
∴AC=x+4, CB=x,AB=8
∵![]()
∴x=6.
∴S△ABC=![]() 24(cm2).
24(cm2).
故答案为:(1)BE=6;(2) S△ABC=24..

练习册系列答案
相关题目