题目内容
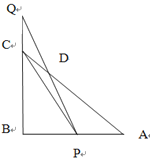
【题目】如图,等腰Rt△ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相等的速度作直线运动,已知点P沿射线AB运动,点Q沿边BC的延长线运动,PQ与直线相交于点D.
(1)设AP的长为x,△PCQ的面积为S,求出S关于x的函数关系式;
(2)当AP的长为何值时,![]() =
=![]() .
.
【答案】(1)S= ;(2)当AP=1+
;(2)当AP=1+![]() 时,
时,![]() =
=![]() .
.
【解析】
(1)本题要分两种情况进行讨论:
①当P在线段AB上;②当P在AB延长线上.
△PCQ都是以CQ为底,PB为高,可据此得出S、x的函数关系式.
(2)先计算出△ABC的面积,然后将其值代入(1)中得出的两个函数式中,即可得出所求的AP的长.
解(1) 解:(1)①当点P在线段AB上时,S△PCQ=![]() CQPB.
CQPB.
∵AP=CQ=x,PB=2-x.
∴S△PCQ=![]() x(2-x).
x(2-x).
即S=![]() (2x-x2)
(2x-x2)![]() ;
;
②当点P在AB延长线上时,S△PCQ=![]() CQPB.
CQPB.
∵AP=CQ=x,PB=x-2.
∴S△PCQ=![]() x(x-2).
x(x-2).
即S=![]() (x2-2x)(x>2);
(x2-2x)(x>2);
∴S= ;
;
(2)由题意得SABC=![]() ×2×2=2
×2×2=2
当![]() =2时,
=2时,
![]() ,原方程无解;
,原方程无解;
![]() =2时
=2时
![]() =1+
=1+![]() ,
,![]() =1-
=1-![]() (舍去)
(舍去)
∴AP=1+![]()
所以当AP=1+![]() 时,
时,![]() =
=![]() .
.

练习册系列答案
相关题目