题目内容
【题目】如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(﹣4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
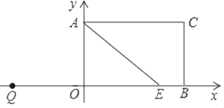
(1)求点E的坐标;
(2)当△PAE是等腰三角形时,求t的值;
(3)以点P为圆心,PA为半径的⊙P随点P的运动而变化,当⊙P与四边形AEBC的边(或边所在的直线)相切时,求t的值.
【答案】(1)点E的坐标为(![]() ,0);(2)当△PAE是等腰三角形时,t的值为(3
,0);(2)当△PAE是等腰三角形时,t的值为(3![]() ﹣2)s或(3
﹣2)s或(3![]() )s或(4+
)s或(4+![]() )s;(3),当⊙P与四边形AEBC的边(或边所在的直线)相切时,t的值为(4﹣
)s;(3),当⊙P与四边形AEBC的边(或边所在的直线)相切时,t的值为(4﹣![]() )秒或4秒或
)秒或4秒或![]() 秒.
秒.
【解析】
(1)由A,B的坐标及∠AEO=30°可得OE=![]() ,即可求出点E的坐标;
,即可求出点E的坐标;
(2)分三种情形①当EA=EP时,EP1=EA=EP2=6,求出t.②当PA=PE时,设P3E=P3E=x,在Rt△AOP3中,32+(![]() -x)2=x2,x=2
-x)2=x2,x=2![]() ,求出t即可.③当AE=AP时,点P在点Q左边,不符合题意.
,求出t即可.③当AE=AP时,点P在点Q左边,不符合题意.
(3)本小题分三种情况讨论:①当PA⊥AE时,⊙P与AE相切;②当PA⊥AC时,⊙P与AC相切;③当PB⊥BC时,⊙P与BC相切;分别求出各种情况的t的值.
(1)∵A(0,3),B(6,0),
∴OA=3,OB=6,
∵∠AEO=30°,
∴OE=![]() OA=3
OA=3![]() ,
,
∴点E的坐标为(3![]() ,0).
,0).
(2)如图1中,
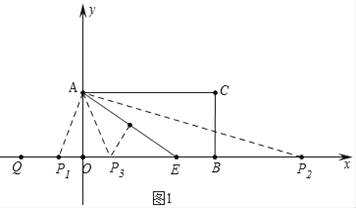
当EA=EP时,EP1=EA=EP2=6,此时t=3![]() ﹣2或3
﹣2或3![]() +10,
+10,
当PA=PE时,设P3E=P3E=x,在Rt△AOP3中,32+(3![]() ﹣x)2=x2,
﹣x)2=x2,
∴x=2![]() ,此时t=4+
,此时t=4+![]()
当AE=AP时,点P在点Q左边,不符合题意.
综上所述,当△PAE是等腰三角形时,t的值为(3![]() ﹣2)s或(3
﹣2)s或(3![]() )s或(4+
)s或(4+![]() )s.
)s.
(3)由题意知,若⊙P与四边形AEBC的边相切,有以下三种情况:
①如图2中,当PA⊥AE时,⊙P与AE相切,
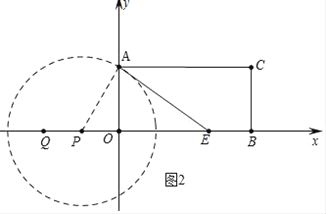
∵∠AEO=30°,AO=3,
∴∠APO=60°,
∴OP=![]() ,
,
∴QP=QO﹣PO=4﹣![]() ,
,
∵点P从点Q(﹣4,0)出发,沿x轴向右以每秒1个单位的速度运动,
∴t=4﹣![]() (秒).
(秒).
②如图3中,当PA⊥AC时,⊙P与AC相切,
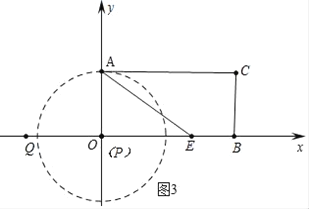
∵QO=4,点P从点Q(﹣4,0)出发,沿x轴向右以每秒1个单位的速度运动,
∴t=4(秒),
③如图4中,当⊙P与BC相切时,
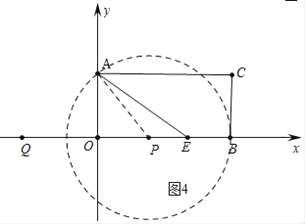
由题意,PA2=PB2=(10﹣t)2,PO2=(t﹣4)2.
于是(10﹣t)2=(t﹣4)2+32.
解得t=![]() (秒),
(秒),
综上所述,当⊙P与四边形AEBC的边(或边所在的直线)相切时,t的值为(4﹣![]() )秒或4秒或
)秒或4秒或![]() 秒.
秒.

 阅读快车系列答案
阅读快车系列答案