题目内容
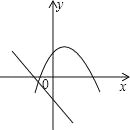
【题目】已知抛物线y=-x2+4交x轴于A,B两点,顶点是C.
(1)求△ABC的面积;
(2)若点P在抛物线y=-x2+4上, 且S△PAB=![]() S△ABC,求点P的坐标。
S△ABC,求点P的坐标。
【答案】(1)8;(2)点P的坐标为:(![]() ,2),(-
,2),(-![]() ,2),(
,2),(![]() ,-2),(-
,-2),(-![]() ,-2).
,-2).
【解析】
(1)根据抛物线的性质得到A(-2,0),B(2,0),C(0,4),所以△ABC是底边为4,高为4的等腰三角形,利用三角形的面积公式可以求出三角形的面积.
(2)根据△PAB的面积是△ABC的面积的一半,得到点P的纵坐标为±2,然后代入抛物线可以求出点P的横坐标,确定点P的坐标.
(1)A(-2,0),B(2,0),C(0,4).
∴S△ABC=![]() ×4×4=8.
×4×4=8.
所以△ABC的面积是8.
(2)∵S△PAB=![]() S△ABC
S△ABC
∴点P的纵坐标为±2,
当y=2时,代入抛物线有:2=-x2+4,得:x=±![]() .
.
当y=-2时,代入抛物线有:-2=-x2+4,得:x=±![]() .
.
所以点P的坐标为:(![]() ,2),(-
,2),(-![]() ,2),(
,2),(![]() ,-2),(-
,-2),(-![]() ,-2).
,-2).

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目