题目内容
【题目】直径为10的⊙O中,弦AB平行于弦CD,若弦AB=8,弦CD=6,则 弦AB,弦CD之间的距离=_____.
【答案】1或7.
【解析】
由于弦AB、CD的具体位置不能确定,故应分两种情况进行讨论:①弦A和CD在圆心同侧;②弦A和CD在圆心异侧;作出半径和弦心距,利用勾股定理和垂径定理求解即可.
①当弦AB和CD在圆心同侧时,如图①,

过点O作OF⊥CD,垂足为F,交AB于点E,连接OA,OC,
∵AB∥CD,
∴OE⊥AB,
∵AB=8,CD=6,
∴AE=4,CF=3,
∵直径为10,
∴OA=OC=5,
∴由勾股定理得:EO=3,OF=4,
∴EF=OF-OE=1;
②当弦AB和CD在圆心异侧时,如图②,
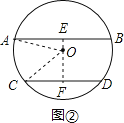
过点O作OE⊥AB于点E,反向延长OE交AD于点F,连接OA,OC,
∵AB∥CD,
∴OF⊥CD,
∵AB=8,CD=6,
∴AE=4,CF=3,
∵OA=OC=5,
∴EO=3,OF=4,
∴EF=OF+OE=7.
故答案为:1或7.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目