题目内容
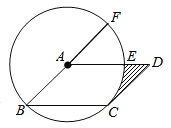
【题目】如图,在△ABC中,点O在BC边上,以OC为半径作⊙O,与AB切于点D,与边BC,AC分别交于点E,F,且弧DE=弧DF.
(1)求证:△ABC是直角三角形.
(2)连结CD交OF于点P,当cos∠B=![]() 时,求
时,求![]() 的值.
的值.

【答案】(1)证明见解析(2)![]()
【解析】
(1)连接OD,根据圆周角定理得出∠ACD=∠BCD,由等腰三角形的性质得出∠OCD=∠ODC,即可得到∠ODC=∠ACD,得出OD∥CA,根据平行线的性质即可得出结论;
(2)连接EF,根据圆周角定理得出∠EFC=90°,进而证得AB∥EF,平行线的性质得出∠CEF=∠B,得出cos∠CEF=cos∠B=![]() ,设OC=OD=OE=a,则EF=
,设OC=OD=OE=a,则EF=![]() a,即可求得CF=
a,即可求得CF=![]() a,由△PDO∽△PCF,即可证得
a,由△PDO∽△PCF,即可证得![]() =
=![]() =
=![]() .
.
(1)证明:如图,连接OD,
∵⊙O与AB切于点D,
∴OD⊥AB,
∴∠BDO=90°,
∵弧DE=弧DF.
∴∠ACD=∠BCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC=∠ACD,
∴OD∥CA,
∴∠BAC=∠BDO=90°,
∴△ABC是直角三角形;
(2)解:连接EF,∵CE是直径,
∴∠EFC=90°,
∴∠BAC=∠EFC,
∴AB∥EF,
∴∠CEF=∠B,
∴cos∠CEF=cos∠B=![]() ,
,
设OC=OD=OE=a,则EF=![]() a,
a,
∴CF=![]() a,
a,
∵OD∥CF,
∴△PDO∽△PCF,
∴![]() =
=![]() =
=![]() .
.


练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
【题目】如下表所示,有A、B两组数:
第1个数 | 第2个数 | 第3个数 | 第4个数 | …… | 第9个数 | …… | 第n个数 | |
A组 | ﹣6 | ﹣5 | ﹣2 | …… | 58 | …… | n2﹣2n﹣5 | |
B组 | 1 | 4 | 7 | 10 | …… | 25 | …… |
(1)A组第4个数是 ;
(2)用含n的代数式表示B组第n个数是 ,并简述理由;
(3)在这两组数中,是否存在同一列上的两个数相等,请说明.