题目内容
【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1≠x2.
(1)求m的取值范围;
(2)如果这个方程的两个实根分别为x1=α,x2=β,且α<β,当m>0时,试比较α,β,2,3的大小,并用“<”连接;
(3)求二次函数y=(x-x1)(x-x2)+m的图像与x轴的交点坐标.
【答案】(1)m>-![]() ;(2)α<2<3<β;(3)(2,0)和(3,0).
;(2)α<2<3<β;(3)(2,0)和(3,0).
【解析】
⑴一元二次方程(x-2)(x-3)=m化为一般形式得:x2-5x+6-m=0,
∵方程有两个不相等的实数根x1、x2,∴△=b2-4ac=(-5)2-4(6-m)=4m+1>0,
解得m>![]()
⑵令m=0,则函数y=(x-1)(x-2)的图象与x轴的交点分别为(1,0),(2,0),故此函数的图象为:
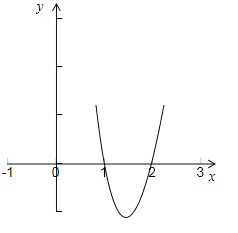
∵m>0,
∴原顶点沿抛物线对称轴向下移动,两个根沿对称轴向两边逐步增大,
∴α<1,β>2.
根据求根公式![]() ,因为m>0.∴
,因为m>0.∴![]()
即 ![]() ;
;
⑶因为一元二次方程![]() 有实数根
有实数根![]() ,且
,且![]() ≠
≠![]() ,
,
所以该一元二次方程可以写成![]() 或者
或者![]()
即:![]()
所以![]() 可以表示成
可以表示成![]()
即:![]() ,所求二次函数的图像与x轴的交点坐标为(2,0)和(3, 0).
,所求二次函数的图像与x轴的交点坐标为(2,0)和(3, 0).

练习册系列答案
相关题目