题目内容
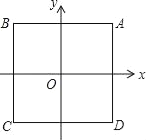
【题目】如图，在平面直角坐标系中，点O是边长为2的正方形ABCD的中心．函数y＝（x﹣h）2的图象与正方形ABCD有公共点，则h的取值范围是_____．
【答案】
【解析】
由于函数y=（x-h）2的图象为开口向上，顶点在x轴上的抛物线，故可先分别得出点A和点B的坐标，因为这两个点为抛物线与与正方形ABCD有公共点的临界点，求出即可得解．
∵点O是边长为2的正方形ABCD的中心，
∴点A和点B坐标分别为（1，1）和（-1，1），
∵函数y=（x-h）2的图象为开口向上，顶点在x轴上的抛物线，
∴其图象与正方形ABCD有公共点的临界点为点A和点B，
把点B坐标代入y=（x-h）2，
得1=（-1-h）2
∴h=0（舍）或h=-2；
把点A坐标代入y=（x-h）2，
得1=（1-h）2
∴h=0（舍）或h=2．
函数y=（x-h）2的图象与正方形ABCD有公共点，则h的取值范围是-2≤h≤2．
故答案为：-2≤h≤2．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
