题目内容
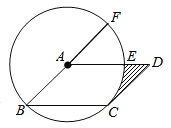
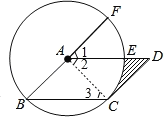
【题目】如图,在ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,交BA的延长线于点F,若弧EF的长为π,则图中阴影部分的面积为______.
【答案】8﹣2π
【解析】
连结AC,如图,设半径为r,先根据切线的性质得∠ACD=90°,再根据平行四边形的性质得AB∥CD,AD∥BC,则∠CAF=90°,∠1=∠B,∠2=∠3,利用∠B=∠3易得∠1=∠2=45°,则根据弧长公式求得r=4,然后根据扇形面积公式,利用S阴影部分=S△ACD﹣S扇形CAE进行计算即可.
连结AC,如图,设半径为r.
∵AB的长为半径的圆恰好与CD相切于点C,∴AC⊥CD,∴∠ACD=90°.
∵四边形ABCD为平行四边形,∴AB∥CD,AD∥BC,∴∠CAF=90°,∠1=∠B,∠2=∠3,而AB=AC,∴∠B=∠3,∴∠1=∠2=45°.
∵![]() 的长为π,∴
的长为π,∴![]() π,解得:r=4.
π,解得:r=4.
在Rt△ACD中,∵∠2=45°,∴AC=CD=4,∴S阴影部分=S△ACD﹣S扇形CAE![]() 4×4
4×4![]() 8﹣2π.
8﹣2π.
故答案为:8﹣2π.

练习册系列答案
相关题目