题目内容
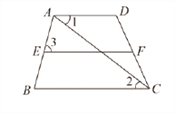
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
【答案】B
【解析】分析: 首先证明∠A=∠DEC,然后可利用AAS判定△ABE≌△ECD,进而可得EC=AB=5m,再求出BE的长,然后利用路程除以速度可得时间
详解: :∵∠AED=90°,
∴∠AEB+∠DEC=90°,
∵ABE=90°,
∴∠A+∠AEB=90°,
∴∠A=∠DEC,
在△ABE和△DCE中
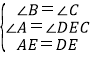 ,
,
∴△ABE≌△ECD(AAS),
∴EC=AB=5m,
∵BC=13m,
∴BE=8m,
∴小华走的时间是8÷1=8(s),
故选:B.
点睛: 此题主要考查了全等三角形的应用,关键是正确判定△ABE≌△ECD.

练习册系列答案
相关题目