题目内容
【题目】如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点P′(x0+5,y0-2).
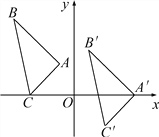
(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积为6.
【答案】(1)A′为(4,0)、B′为(1,3)、C′为(2,-2);
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位);
(3)△A′B′C′的面积为6.
【解析】试题分析: (1)根据点P(x0,y0)经平移后对应点为P′(x0+5,y0-2)可得A,B,C三点的坐标变化规律,进而可得答案,
(2)根据点的坐标的变化规律可得△ABC先向右平移5个单位,再向下平移2个单位,(3)把△A′B′C′放在一个矩形内,利用矩形的面积减去周围多余三角形的面积即可
试题解析:(1)A′为(4,0),B′为(1,3),C′为(2,-2),
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位),
(3)△A′B′C′的面积为6.

练习册系列答案
相关题目


