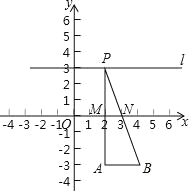题目内容
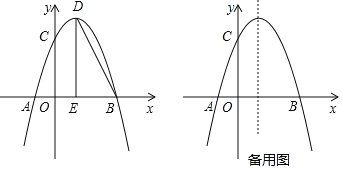
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B,与y轴交于点C,且OA=2,OB=OC=6,点D是抛物线的顶点,过点D作x轴的垂线,垂足为E.
(1)求抛物线的解析式及点D的坐标;
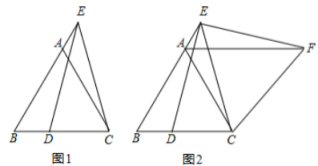
(2)连接BD,若点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标:
(3)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请求出点Q的坐标.
【答案】(1)![]() ,D(2,8);(2)F点的坐标为(﹣1,
,D(2,8);(2)F点的坐标为(﹣1,![]() )或(﹣3,
)或(﹣3,![]() );(3)满足条件的点Q有两个,其坐标分别为(2,﹣2+2
);(3)满足条件的点Q有两个,其坐标分别为(2,﹣2+2![]() )或(2,﹣2﹣2
)或(2,﹣2﹣2![]() ).
).
【解析】
(1)由OA=2,OB=OC=6,写出A、B、C的坐标,利用待定系数法可求得抛物线解析式,再求其顶点D即可;
(2)过F作FG⊥x轴于点G,可设出F点坐标,利用△FBG∽△BDE,由相似三角形的性质可得到关于F点坐标的方程,可求得F点的坐标;
(3)由于M、N两点关于对称轴对称,可知点P为对称轴与x轴的交点,点Q在对称轴上,可设出Q点的坐标,则可表示出M的坐标,代入抛物线解析式可求得Q点的坐标.
解:(1)∵OA=2,OB=OC=6,∴A(﹣2,0),B(6,0),C(0,6),
∴可设抛物线解析式为y=a(x+2)(x﹣6),
把C点的坐标代入可得6=﹣12a,解得:a=![]() ,
,
∴抛物线解析式为y=![]() (x+2)(x﹣6)=
(x+2)(x﹣6)=![]() x2+2x+6;
x2+2x+6;
∴D(2,8);
(2)如图1,过F作FG⊥x轴于点G,设F(m,![]() m2+2m+6),
m2+2m+6),
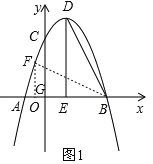
则FG=|![]() m2+2m+6|.
m2+2m+6|.
∵B(6,0),D(2,8),
∴E(2,0),BE=4,DE=8,OB=6,
∴BG=6﹣m,
∵∠FBA=∠BDE,∠FGB=∠BED=90°,
∴△FBG∽△BDE,∴![]() .
.
∴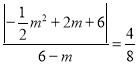 ,
,
当点F在x轴上方时,有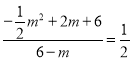 ,
,
解得:x=﹣1或x=6(舍去),
此时F点的坐标为(﹣1,![]() ),
),
当点F在x轴下方时,有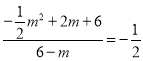 ,
,
解得:x=﹣3或x=6(舍去),
此时F点的坐标为(﹣3,![]() ),
),
综上可知F点的坐标为(﹣1,![]() )或(﹣3,
)或(﹣3,![]() );
);
(3)如图2,设对角线MN、PQ交于点O',
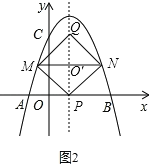
∵点M、N关于抛物线对称轴对称,且四边形MPNQ为正方形,
∴点P为抛物线对称轴与x轴的交点,点Q在抛物线的对称轴上,
QO'=MO'=PO'=NO',PQ⊥MN,
设Q(2,2n),则M坐标为(2﹣n,n).
∵点M在抛物线y=![]() x2+2x+6的图象上,
x2+2x+6的图象上,
∴n=![]() (2﹣n)2+2(2﹣n)+6,
(2﹣n)2+2(2﹣n)+6,
解得:n=﹣1+![]() 或n=﹣1﹣
或n=﹣1﹣![]() ,
,
∴满足条件的点Q有两个,其坐标分别为(2,﹣2+2![]() )或(2,﹣2﹣2
)或(2,﹣2﹣2![]() ).
).

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案