Question

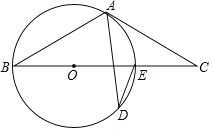
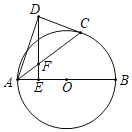
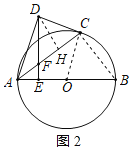
【题目】如图，AB是⊙O的直径，点C在半圆上，点D在圆外，DE⊥AB于点E交AC于点F，且DF＝CD

（1）求证：CD是⊙O的切线；

（2）若点F是AC的中点，DF＝2EF＝2，求⊙O半径．

Answer 1

【答案】（1）详见解析；（2）4．

【解析】

（1）连接OC，易证∠BAC+∠AFE＝90°，由等腰三角形的性质得出∠DFC＝∠DCF，∠BAC＝∠OCA，由∠DFC＝∠AFE，推出∠DCF+∠OCA＝90°，即可得出结论；

（2）连接BC，作DH⊥AC于点H，由等腰三角形的性质得出FH＝CH＝CF，由已知得出AF＝CF＝AC，FH＝AC，EF＝，易证△AFE∽△DFH，得出＝，求出AC＝4，则AF＝AC＝2，由勾股定理得出AE＝＝3，由AB是⊙O的直径，得出∠ACB＝∠AED＝90°，易证△BAC∽△FAE，得出＝，求出AB＝8，即可得出结果．

（1）证明：连接OC，如图1所示：

∵DE⊥AB，

∴∠AED＝90°，

∴∠BAC+∠AFE＝90°，

∵DF＝CD，

∴∠DFC＝∠DCF，

∵OA＝OC，

∴∠BAC＝∠OCA，

∵∠DFC＝∠AFE，

∴∠DCF+∠OCA＝90°，

∴∠OCD＝90°，

∴OC⊥CD，

∴CD是⊙O的切线；

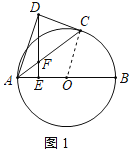
（2）解：连接BC，作DH⊥AC于点H，如图2所示：

∵DF＝CD，

∴FH＝CH＝CF，

∵点F是AC的中点，DF＝2EF＝2，

∴AF＝CF＝AC，FH＝AC，EF＝，

∵∠AED＝∠DHF＝90°，∠AFE＝∠DFH，

∴△AFE∽△DFH，

∴＝，

∴AFFH＝DFEF，

即：AC×AC＝2×，

解得：AC＝±4（负值不合题意舍去），

∴AF＝AC＝2，

∴AE＝＝＝3，

∵AB是⊙O的直径，

∴∠ACB＝∠AED＝90°，

∵∠BAC＝∠FAE，

∴△BAC∽△FAE，

∴＝，

即：＝，

解得：AB＝8，

∴⊙O半径＝AB＝×8＝4．