题目内容
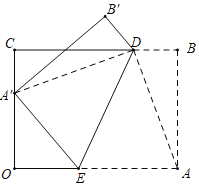
【题目】如图,长方形OABC中,OA=8,AB=6,点D在边BC上,且CD=3DB,点E是边OA上一点,连接DE,将四边形ABDE沿DE折叠,若点A的对称点A′恰好落在边OC上,则OE的长为_____.
【答案】3
【解析】
首先根据长方形性质得出BC=OA=8,OC=AB=6,∠C=∠B=∠O=90°,然后结合题意得出CD=AB,接着利用折叠性质进一步证明出Rt△A′CD与Rt△DBA全等,由此得到A′O=4,最后在Rt△OEA′中,利用勾股定理进一步求解即可.
∵四边形OABC是长方形,
∴BC=OA=8,OC=AB=6,∠C=∠B=∠O=90°,
∵CD=3DB,
∴BC=CD+BD=4BD,
∴BD=2,
∴CD=6,
∴CD=AB,
∵将四边形ABDE沿DE折叠,若点A的对称点A′恰好落在边OC上,
∴A′D=AD,A′E=AE,
在Rt△A′CD与Rt△DBA中,
∵CD=AB,A′D=AD,
∴Rt△A′CD≌Rt△DBA(HL),
∴A′C=BD=2,
∴A′O=4,
在Rt△OEA′中,
∵A′O2+OE2=A′E2,
∴42+OE2=(8OE)2,
∴OE=3,
故答案为:3.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目