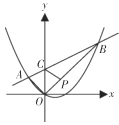
ЬтФПФкШн
ЁОЬтФПЁПШчЭМХзЮяЯпyЃНax2+ax+cЃЈaЁй0ЃЉгыxжсЕФНЛЕуЮЊAЁЂBЃЈAдкBЕФзѓБпЃЉЧвABЃН3ЃЌгыyжсНЛгкCЃЌШєХзЮяЯпЙ§ЕуEЃЈЉ1ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкxжсЕФЯТЗНЪЧЗёДцдквЛЕуPЪЙЕУЁїPBCЕФУцЛ§ЮЊ3ЃПШєДцдкЧѓГіPЕуЕФзјБъЃЌВЛДцдкЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєDЮЊдЕуЙигкAЕуЕФЖдГЦЕуЃЌFЕузјБъЮЊЃЈ0ЃЌ1.5ЃЉЃЌНЋЁїCEFШЦЕуCа§зЊЃЌдка§зЊЙ§ГЬжаЃЌЯпЖЮDEгыBFЪЧЗёДцдкФГжжЙиЯЕЃЈЪ§СПЁЂЮЛжУЃЉЃПЧыжИГіВЂжЄУїФуЕФНсТлЃЎ
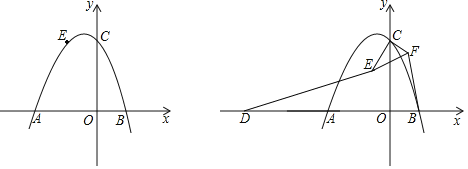
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2Љx+2ЃЛЃЈ2ЃЉДцдкЃЌPЃЈ3ЃЌЉ10ЃЉЃЛЃЈ3ЃЉDEЁЭBFЧвDEЃН2BFЃЌжЄУїМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЕУГіХзЮяЯпЕФЖдГЦжсЮЊxЃН![]() ЃН
ЃН![]() ЃЌгжгыxжсЕФНЛЕуЮЊAЁЂBЃЈAдкBЕФзѓБпЃЉЧвABЃН3ЃЌЧѓГіAЁЂBЕуЕФзјБъЃЌАбAЁЂEзјБъДњШы
ЃЌгжгыxжсЕФНЛЕуЮЊAЁЂBЃЈAдкBЕФзѓБпЃЉЧвABЃН3ЃЌЧѓГіAЁЂBЕуЕФзјБъЃЌАбAЁЂEзјБъДњШы![]() ПЩЕУaЁЂcЕФжЕЃЌМЬЖјЧѓЕУХзЮяЯпЕФНтЮіЪНЃЛ
ПЩЕУaЁЂcЕФжЕЃЌМЬЖјЧѓЕУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвђЮЊSЁїABCЃН3ЃЌЁїPBCЕФУцЛ§ЪЧ3ЃЌЫЕУїЕуPвЛЖЈдкЙ§AЦНаагкBCЕФжБЯпЯпЃЌЧввЛЖЈЪЧгыХзЮяЯпЕФНЛЕуЃЌвђДЫЧѓГіЙ§AЕуЦНаагкBCЕФжБЯпЃЌгыХзЮяЯпСЊСЂНјвЛВНЧѓЕУД№АИЃЛ
ЃЈ3ЃЉСЌНгDCЁЂBCЃЌжЄУїЁїCDEЁзЁїCBFЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪКЭа§зЊЕФаджЪМДПЩНтОіЮЪЬтЃЎ
НтЃКЃЈ1ЃЉвђЮЊХзЮяЯп![]() ЃЈaЁй0ЃЉЕФЖдГЦжсЪЧxЃН
ЃЈaЁй0ЃЉЕФЖдГЦжсЪЧxЃН![]() ЃН
ЃН![]() ЃЌABЃН3ЃЌ
ЃЌABЃН3ЃЌ
ЫљвдAЁЂBСНЕуЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЁЂЃЈ1ЃЌ0ЃЉЃЌ
гжвђЮЊEЃЈЉ1ЃЌ2ЃЉдкХзЮяЯпЩЯЃЌ
АбЕуAЃЈЉ2ЃЌ0ЃЉЁЂEЃЈЉ1ЃЌ2ЃЉДњШы![]()
![]()
НтЕУaЃНЉ1ЃЌcЃН2ЃЌ
Ыљвд![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЫљЪОЃЌЙ§AзїBCЕФЦНааЯпНЛХзЮяЯпгкЕуPЃЈЦЊЗљгаЯоЃЌPЕуЮДФмЯдЪОдкЭМжаЃЉЃЌ
СюxЃН0ЃЌдђyЃН2
ЙЪЕуCзјБъЪЧЃЈ0ЃЌ2ЃЉ,
ЁпЩшжБЯпBCЕФНтЮіЪНЮЊЃКyЃНkx+bЃЌ
BЕузјБъЮЊЃКЃЈ1ЃЌ0ЃЉЃЌCЕузјБъЮЊЃЛЃЈ0ЃЌ2ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрyЃНЉ2x+2ЃЌ
ЁпAзїBCЕФЦНааЯпНЛХзЮяЯпгкЕуPЃЌ
ЁрyЃНЉ2x+bЃЌНЋAЃЈЉ2ЃЌ0ЃЉДњШыНтЮіЪНМДПЩЕУГіЃЌ
ЫљвдЙ§AЕуЕФжБЯпЮЊyЃНЉ2xЉ4ЃЌ
ЁрСНКЏЪ§ЕФНЛЕузјБъЮЊЃК
гЩЉx2Љx+2ЃНЉ2xЉ4ЃЌ
НтЕУx1ЃНЉ2ЃЈЩсШЅЃЉЃЌx2ЃН3ЃЌ
ЫљвдгыХзЮяЯпЕФНЛЕуPЮЊЃЈ3ЃЌЉ10ЃЉЃЛ
ЃЈ3ЃЉШчЭМЃЈ3ЃЉЫљЪОЃЌСЌНгDCЁЂBCЃЌ
гЩЬтвтПЩжЊЃКЕуDЃЈЉ4ЃЌ0ЃЉЃЌFЃЈ0ЃЌ1.5ЃЉЃЌ
ЁрDCЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
BCЃН![]() ЃЌ
ЃЌ
CEЃН![]() ЃЌ
ЃЌ
CFЃН![]() ЃЌ
ЃЌ
EFЃН![]()
ЕУ![]() ЃЌ
ЃЌ![]()
гжЁпМаНЧЁЯDCEЃНЁЯBCFЃЌ
ЁрЁїCDEЁзЁїCBFЃЌЖјЁЯECFЃН90ЁуЃЌ
Ёр![]() ЃЌCEЁЭCFЃЌ
ЃЌCEЁЭCFЃЌ
ЁрDEЁЭBFЧвDEЃН2BFЃЎ
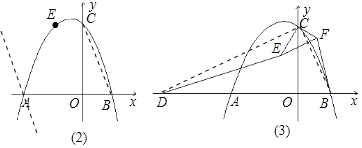

 ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ
ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ