题目内容
【题目】如图，点O为平面直角坐标系的原点，点A在x轴上，△OAB是边长为4的等边三角形，以O为旋转中心，将△OAB按顺时针方向旋转60°，得到△OA′B′，那么点A′的坐标为（ ）
A. （2，2
） B. （﹣2，4） C. （﹣2，2
） D. （﹣2，2
）
【答案】D
【解析】分析：作BC⊥x轴于C，如图，根据等边三角形的性质得
则易得A点坐标和O点坐标，再利用勾股定理计算出
然后根据第二象限点的坐标特征可写出B点坐标；由旋转的性质得
则点A′与点B重合，于是可得点A′的坐标．
详解：作BC⊥x轴于C，如图，
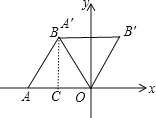
∵△OAB是边长为4的等边三角形
∴
∴A点坐标为(4,0),O点坐标为(0,0)，
在Rt△BOC中, 
∴B点坐标为
∵△OAB按顺时针方向旋转
,得到△OA′B′，
∴
∴点A′与点B重合,即点A′的坐标为
故选D.
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
