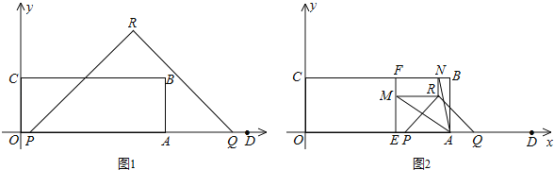题目内容
【题目】如图,在平面直角坐标系xOy中,已知直线AB:y![]() x+4交x轴于点A,交y轴于点B.直线CD:y
x+4交x轴于点A,交y轴于点B.直线CD:y![]() x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
(1)直接写出点B和点D的坐标;
(2)若点P是射线MD上的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B、E、P、M为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点E的坐标;若不存在,说明理由.

【答案】(1)B(0,4),D(0,-1);(2)S![]() (x>-5);(3)存在,满足条件的点E的坐标为(8,
(x>-5);(3)存在,满足条件的点E的坐标为(8,![]() )或(﹣8,
)或(﹣8,![]() )或(﹣2,
)或(﹣2,![]() ).
).
【解析】
(1)利用y轴上的点的坐标特征即可得出结论;
(2)先求出点M的坐标,再分两种情况讨论:①当P在y轴右边时,用三角形的面积之和即可得出结论,②当P在y轴左边时,用三角形的面积之差即可得出结论;
(3)分三种情况利用对角线互相平分的四边形是平行四边形和线段的中点坐标的确定方法即可得出结论.
(1)∵点B是直线AB:y![]() x+4与y轴的交点坐标,∴B(0,4).
x+4与y轴的交点坐标,∴B(0,4).
∵点D是直线CD:y![]() x﹣1与y轴的交点坐标,∴D(0,﹣1);
x﹣1与y轴的交点坐标,∴D(0,﹣1);
(2)如图1.由 ,解得:
,解得: .
.
∵直线AB与CD相交于M,∴M(﹣5,![]() ).
).
∵B(0,4),D(0,﹣1),∴BD=5.
∵点P在射线MD上,∴分两种情况讨论:
①当P在y轴右边时,即x≥0时,S=S△BDM+S△BDP![]() 5(5+x)
5(5+x)![]() ;
;
②当P在y轴左边时,即-5<x<0时,S=S△BDM-S△BDP![]() 5(5-|x|)
5(5-|x|)![]() ;
;
综上所述:S=![]() (x>-5).
(x>-5).
(3)如图2,由(1)知,S![]() ,当S=20时,
,当S=20时,![]() 20,∴x=3,∴P(3,﹣2).
20,∴x=3,∴P(3,﹣2).
分三种情况讨论:
①当BP是对角线时,取BP的中点G,连接MG并延长取一点E'使GE'=GM,设E'(m,n).
∵B(0,4),P(3,﹣2),∴BP的中点坐标为(![]() ,1).
,1).
∵M(﹣5,![]() ),∴
),∴![]() 1,∴m=8,n
1,∴m=8,n![]() ,∴E'(8,
,∴E'(8,![]() );
);
②当AB为对角线时,同①的方法得:E(﹣8,![]() );
);
③当MP为对角线时,同①的方法得:E'(﹣2,![]() ).
).
综上所述:满足条件的点E的坐标为(8,![]() )、(﹣8,
)、(﹣8,![]() )、(﹣2,
)、(﹣2,![]() ).
).