ЬтФПФкШн
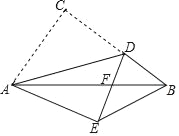
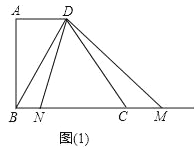
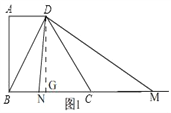
ЁОЬтФПЁПвбжЊЃЌдкЬнаЮABCDжаЃЌADЁЮBCЃЌЁЯA=90ЁуЃЌAD=2ЃЌAB=4ЃЌBC=5ЃЌдкЩфЯпBCШЮШЁвЛЕуMЃЌСЊНсDMЃЌзїЁЯMDN=ЁЯBDCЃЌЁЯMDNЕФСэвЛБпDNНЛжБЯпBCгкЕуNЃЈЕуNдкЕуMЕФзѓВрЃЉЃЎ
ЃЈ1ЃЉЕБBMЕФГЄЮЊ10ЪБЃЌЧѓжЄЃКBDЁЭDMЃЛ
ЃЈ2ЃЉШчЭМЃЈ1ЃЉЃЌЕБЕуNдкЯпЖЮBCЩЯЪБЃЌЩшBN=xЃЌBM=yЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЫќЕФЖЈвхгђЃЛ
ЃЈ3ЃЉШчЙћЁїDMNЪЧЕШбќШ§НЧаЮЃЌЧѓBNЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉy=![]() ЃЌ0ЁмxЃМ4ЃЛЃЈ3ЃЉBN=0Лђ1Лђ2
ЃЌ0ЁмxЃМ4ЃЛЃЈ3ЃЉBN=0Лђ1Лђ2![]() Љ4ЃЎ
Љ4ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃК
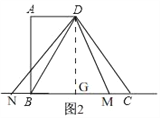
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуDзїDGЁЭBCгкGЃЌгЩвбжЊвзЕУЫФБпаЮABGDЪЧОиаЮЃЌдђBG=AD=2ЃЌDG=AB=4ЃЌгЩBC=5ПЩЕУCG=3ЃЌгЩЙДЙЩЖЈРэПЩЕУCD=5ЃЌНсКЯBM=10ПЩЕУCM=BM-BC=5=BC=CDЃЌгЩДЫПЩЕУЁїBDMЪЧжБНЧШ§НЧаЮЃЌДгЖјПЩЕУBDЁЭDMЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌгЩЃЈ1ЃЉжаCD==5=BCПЩЕУЁЯBDC=ЁЯDBCНсКЯЁЯMDN=ЁЯBDCМДПЩЕУЕНЁЯDBC=ЁЯMDNЃЌдйНсКЯЁЯBMD=ЁЯDMNПЩЕУЁїMDNЁзЁїMBDЃЌДгЖјПЩЕУDM2=BMЁСMNНсКЯDM2=DG2+MG2=16+ЃЈyЉ2ЃЉ2ЃЌMN=BMЉBN=yЉxЃЌПЩЕУ16+ЃЈyЉ2ЃЉ2=yЃЈyЉxЃЉЃЌећРэПЩЕУy=![]() ЃЌНсКЯЕуNдкЯпЖЮBCЩЯПЩЕУxЕФШЁжЕЗЖЮЇЪЧЃК
ЃЌНсКЯЕуNдкЯпЖЮBCЩЯПЩЕУxЕФШЁжЕЗЖЮЇЪЧЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЗжЃКЂёЁЂDN=DMЃЛIIЁЂDM=MNЃЛIIIЁЂMN=DNШ§жжЧщПіНсКЯвбжЊЬѕМўКЭЧАУцЫљЕУНсТлНјааЗжЮіМЦЫуМДПЩ.
ЪдЬтНтЮіЃК
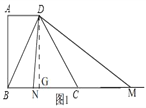
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуDзїDGЁЭBCгкGЃЌ
ЁрЁЯBGD=90ЁуЃЌ
ЁпЁЯA=90ЁуЃЌЬнаЮABCDжаЃЌADЁЮBCЃЌ
ЁрЁЯABC=90ЁуЃЌ
ЁрЫФБпаЮABGDЪЧОиаЮЃЌBG=AD=2ЃЌDG=AB=4ЃЌ
ЁпBC=5ЃЌ
ЁрCG=BCЉBG=3ЃЌ
дкRtЁїCDGжаЃЌИљОнЙДЙЩЖЈРэЕУЃЌCD=5ЃЌ
ЁпBM=10ЃЌ
ЁрCM=BMЉBC=5=BC=CDЃЌ
ЁрЁїBDMЪЧжБНЧШ§НЧаЮЃЌ
ЁрBDЁЭDMЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЃЌCD=5=BCЃЌ
ЁрЁЯBDC=ЁЯDBCЃЌ
ЁпЁЯMDN=ЁЯBDCЃЌ
ЁрЁЯDBC=ЁЯMDNЃЌ
ЁпЁЯBMD=ЁЯDMNЃЌ
ЁрЁїMDNЁзЁїMBDЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрDM2=BMЁСMN
дкRtЁїDMGжаЃЌИљОнЙДЙЩЖЈРэЕУЃЌDM2=DG2+MG2=16+ЃЈyЉ2ЃЉ2ЃЌ
ЁпMN=BMЉBN=yЉxЃЌ
Ёр16+ЃЈyЉ2ЃЉ2=yЃЈyЉxЃЉЃЌ
Ёрy=![]() ЃЌ
ЃЌ
гжЁпЕуNдкЯпЖЮBCЩЯЃЌ
Ёр0ЁмxЃМ4ЃЛ
ЃЈ3ЃЉЁпЁїDMNЪЧЕШбќШ§НЧаЮЃЌ
ЁрЂёЁЂЕБDN=DMЪБЃЌШчЭМ1ЃЌNG=MGЃЌ
ЁпNG=2ЉxЃЌMG=yЉ2ЃЌ
Ёр2Љx=yЉ2ЃЌ
Ёрx+y=4ЂкЃЌ
гЩЃЈ2ЃЉжЊЃЌy=![]() ЃЌ
ЃЌ
ЁрyЃЈ4ЉxЃЉ=20Ђй
СЊСЂЂйЂкЃЌНтЕУx=Љ![]() Љ4ЃЈЩсЃЉЛђx=
Љ4ЃЈЩсЃЉЛђx=![]() Љ4ЃЌ
Љ4ЃЌ
МДЃКBN=![]() -4ЃЌ
-4ЃЌ
ЂђЁЂЕБDM=MNЪБЃЌ
ЁрЁЯMDN=ЁЯDNMЃЌ
ЁпЁЯCBD=ЁЯMDNЃЌ
ЁрЁЯCBD=ЁЯDNMЃЌ
ЁрЕуNгыЕуBжиКЯЃЌ
ЁрBN=0ЃЌ
ЂѓЁЂЕБMN=DNЪБЃЌ
ЁрЁЯMDN=ЁЯDMNЃЌ
ЁпЁЯDBC=ЁЯMDNЃЌ
ЁрЁЯDBC=ЁЯDMNЃЌ
ЁрDM=BDЃЌ
дкRtЁїABDжаЃЌИљОнЙДЙЩЖЈРэЕУЃЌBD2=AD2+AB2=20ЃЌ
ЁпDM2=16+ЃЈBMЉ2ЃЉ2ЃЌ
Ёр20=16+ЃЈBMЉ2ЃЉ2ЃЌ
ЁрBM=0ЃЈЩсШЅЃЉЛђBM=4ЃЌ
ЁрШчЭМ2ЃЌ
ЕуMдкЯпЖЮBCЩЯЃЌ
ЭЌЃЈ2ЃЉЕФЗНЗЈЕУЃЌ16+ЃЈBMЉ2ЃЉ2=BMЃЈBMЉBNЃЉЂлЃЌ
ЁпMN=BN+BMЂмЃЌ
СЊСЂЂлЂмНтЕУЃЌBN=1ЃЎ
МДЃКBN=0Лђ1Лђ![]() Љ4ЃЎ
Љ4ЃЎ

 аТПЮБъНзЬндФЖСбЕСЗЯЕСаД№АИ
аТПЮБъНзЬндФЖСбЕСЗЯЕСаД№АИ