题目内容
【题目】(本题满分10分)
某校为了解“阳光体育”活动的开展情况,从全校![]() 名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
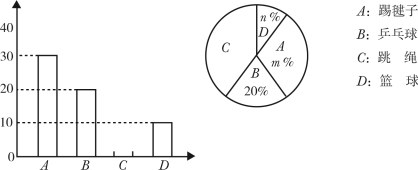
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,![]() = ,
= ,![]() = ,表示区域
= ,表示区域![]() 的圆心角为 °;
的圆心角为 °;
(3)全校学生中喜欢篮球的人数大约有多少?
【答案】(1)100人,图形详见解析;
【解析】
试题(1)用B组频数除以其所占的百分比即可求得样本容量;
(2)用A组人数除以总人数即可求得m值,用D组人数除以总人数即可求得n值;
(3)用总人数乘以D类所占的百分比即可求得全校喜欢篮球的人数.
试题解析:解:(1)20÷20%=100(人),
喜欢跳绳的有100﹣30﹣20﹣10=40(人),
故答案为:100;条形统计图为:
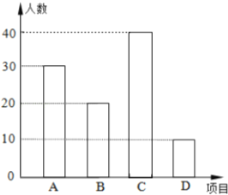
(2)∵A组有30人,D组有10人,共有100人,
∴A组所占的百分比为:30%,D组所占的百分比为10%,
∴m=30,n=10;
表示区域C的圆心角为![]() ×360°=144°,
×360°=144°,
故答案为:30;10;144°;
(3)∵全校共有2000人,喜欢篮球的占10%,
∴喜欢篮球的有2000×10%=200人.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目