题目内容
【题目】如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2![]() ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
【答案】4或4![]() .
.
【解析】
①当AF<![]() AD时,由折叠的性质得到A′E=AE=2
AD时,由折叠的性质得到A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,过E作EH⊥MN于H,由矩形的性质得到MH=AE=2
,AF=A′F,∠FA′E=∠A=90°,过E作EH⊥MN于H,由矩形的性质得到MH=AE=2![]() ,根据勾股定理得到A′H=
,根据勾股定理得到A′H=![]() ,根据勾股定理列方程即可得到结论;②当AF>
,根据勾股定理列方程即可得到结论;②当AF>![]() AD时,由折叠的性质得到A′E=AE=2
AD时,由折叠的性质得到A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,过A′作HG∥BC交AB于G,交CD于H,根据矩形的性质得到DH=AG,HG=AD=6,根据勾股定理即可得到结论.
,AF=A′F,∠FA′E=∠A=90°,过A′作HG∥BC交AB于G,交CD于H,根据矩形的性质得到DH=AG,HG=AD=6,根据勾股定理即可得到结论.
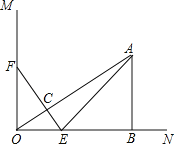
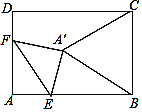
①当AF<![]() AD时,如图1,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
AD时,如图1,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,

则A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,
,AF=A′F,∠FA′E=∠A=90°,
设MN是BC的垂直平分线,
则AM=![]() AD=3,
AD=3,
过E作EH⊥MN于H,
则四边形AEHM是矩形,
∴MH=AE=2![]() ,
,
∵A′H=![]() ,
,
∴A′M=![]() ,
,
∵MF2+A′M2=A′F2,
∴(3-AF)2+(![]() )2=AF2,
)2=AF2,
∴AF=2,
∴EF=![]() =4;
=4;
②当AF>![]() AD时,如图2,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
AD时,如图2,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上,
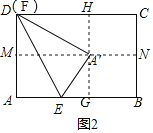
则A′E=AE=2![]() ,AF=A′F,∠FA′E=∠A=90°,
,AF=A′F,∠FA′E=∠A=90°,
设MN是BC的垂直平分线,
过A′作HG∥BC交AB于G,交CD于H,
则四边形AGHD是矩形,
∴DH=AG,HG=AD=6,
∴A′H=A′G=![]() HG=3,
HG=3,
∴EG=![]() =
=![]() ,
,
∴DH=AG=AE+EG=3![]() ,
,
∴A′F=![]() =6,
=6,
∴EF=![]() =4
=4![]() ,
,
综上所述,折痕EF的长为4或4![]() ,
,
故答案为:4或4![]() .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目