��Ŀ����
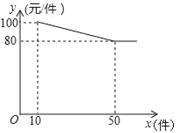
����Ŀ��ij��������˾��������50�����г���������������Ϊÿ��ÿ��200Ԫʱ��ȫ������������ÿ���10Ԫ�����ȥ�ij��ͼ���2����
��1���������߶���Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ��
��2����˾�쵼ϣ��������ﵽ10200Ԫ������Ϊ�ܷ�ʵ�֣����ܣ������ʱ����������ܣ���˵�����ɣ�
��3�������ճ�ά��Ҫһ�����ã���֪�����ÿ��ά����Ϊ100Ԫ��δ����ij���ά����Ϊ50Ԫ�������Ϊ����Ԫʱ����˾������ǡ��Ϊ5500Ԫ������������һά���ѣ���
���𰸡���1����������20Ԫ��30Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ����2�������治�ܴﵽ10200Ԫ����3�������Ϊ250Ԫʱ����˾������ǡ��Ϊ5500Ԫ��
��������
��1����������xԪ����ÿ�տ������50![]() ���������������ÿ��������������������ɵó�����x��һԪ���η��̣���֮���ɵó����ۣ�
���������������ÿ��������������������ɵó�����x��һԪ���η��̣���֮���ɵó����ۣ�
��2�����������ÿ��������������������ɵó�����x��һԪ���η��̣��ɸ����б�ʽ����0�����ɵó���һԪ���η����⣬�����ɵó������治�ܴﵽ10200Ԫ��
��3�����������ÿ����������������������������ά���ѣ����ɵó�����x��һԪ���η��̣���֮���ɵó����ۣ�
��1����������xԪ����ÿ�տ������50��![]() ������
������
�������⣬�ã���200+x����50��![]() ����10120��
����10120��
�������ã�x2��50x+600��0��
��ã�x1��20��x2��30��
�𣺵�������20Ԫ��30Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ��
��2��������ʵ�֣�
�����⣬�ã���200+x����50��![]() ����10200��
����10200��
�������ã�x2��50x+1000��0��
��![]() ������50��2��4��1��1000����1500��0��
������50��2��4��1��1000����1500��0��
����һԪ���η����⣬
�������治�ܴﵽ10200Ԫ��
��3�������⣬�ã���200+x����50��![]() ����100��50��
����100��50��![]() ����50��
����50��![]() ��5500��
��5500��
�������ã�x2��100x+2500��0��
��ã�x1��x2��50��
��200+x��250��
�𣺵����Ϊ250Ԫʱ����˾������ǡ��Ϊ5500Ԫ��