题目内容
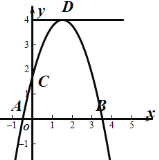
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(2)我们规定:对于直线![]() ,直线
,直线![]() ,若
,若![]() ,则直线
,则直线![]() ;反过来也成立.请根据这个规定解决下列问题:
;反过来也成立.请根据这个规定解决下列问题:
①直线![]() 与直线
与直线![]() 是否垂直?并说明理由;
是否垂直?并说明理由;
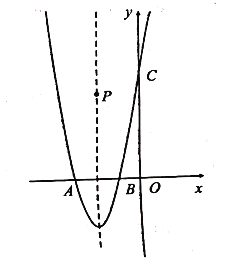
②若点![]() 是抛物线
是抛物线![]() 的对称轴上一动点,是否存在点
的对称轴上一动点,是否存在点![]() 与点
与点![]() ,点
,点![]() 构成以
构成以![]() 为直角边的直角三角形?若存在,请求出点
为直角边的直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;(2) ①不垂直,理由详见解析;②存在,点
;(2) ①不垂直,理由详见解析;②存在,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)令![]() ,求出x的值,根据点
,求出x的值,根据点![]() 在点
在点![]() 的左侧求出A的坐标,令
的左侧求出A的坐标,令![]() ,求出y的值即可求出C的坐标;
,求出y的值即可求出C的坐标;
(2)①分别求出两条直线的斜率,然后根据两斜率的积不等于-1即可证明两直线不垂直;②根据点![]() ,点
,点![]() 的坐标求出直线AC的函数表达式,然后对
的坐标求出直线AC的函数表达式,然后对![]() 时与
时与![]() 时两种情况分别讨论计算即可.
时两种情况分别讨论计算即可.
解:
(1)当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]()
∵点![]() 在点
在点![]() 的左侧,
的左侧,
∴点![]() 坐标为
坐标为![]()
当![]() 时,
时,![]()
∴点![]() 坐标为
坐标为![]() .
.
(2)①不垂直;由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]()
∵![]()
∴直线![]() 与直线
与直线![]() 不垂直;
不垂直;
②存在.
∵![]()
∴抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
设直线![]() ,根据题意得
,根据题意得![]() ,解得
,解得![]()
∴直线![]() 的函数表达式为
的函数表达式为![]()
分两种情况:Ⅰ)当![]() 时,如图,根据新定义可设
时,如图,根据新定义可设![]()
∵点![]() 坐标为
坐标为![]()
∴![]()
∴![]()
直线![]() 的函数表达式为
的函数表达式为![]() ,当
,当![]() 时,
时,![]()
此时点![]() 坐标为
坐标为![]() ;
;
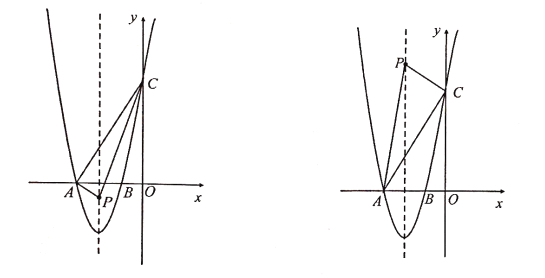
Ⅱ)当![]() 时,如图,根据新定义可设
时,如图,根据新定义可设![]()
∵点![]() 坐标为
坐标为![]()
∴![]() ,
,![]()
∴直线![]() 的函数表达式为
的函数表达式为![]() ,当
,当![]() 时,
时,![]() ,
,
此时点![]() 坐标为
坐标为![]() ;
;
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

【题目】小华是数学兴趣小组的一名成员,他在学过二次函数的图像与性质之后,对![]() 的图像与性质进行了探究,探究过程如下,请你补充完整.
的图像与性质进行了探究,探究过程如下,请你补充完整.
(1)小刚通过计算得到几组对应的数值如下
| … |
|
|
|
|
|
| 0 | 1 |
| 2 | 3 | 4 | 5 | … |
| … |
| 0 | 4 | 6 |
| 6 | 4 | 6 |
| 6 | 4 | 0 |
| … |
填空:自变量的取值范围是__________________,![]() __________.
__________.
(2)在如图所示的平面直角坐标系中,描出上表中各组对应数值的点,并根据描出的点,画出该函数的图像.
(3)请你根据画出的图像,写出此函数的两条性质;
①__________________________________________;
②__________________________________________.
(4)直线![]() 经过
经过![]() ,若关于
,若关于![]() 的方程
的方程![]() 有4个不相等的实数根,则
有4个不相等的实数根,则![]() 的取值范围为_________.
的取值范围为_________.

【题目】表中所列 ![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中 ![]()
x | … |
|
|
|
|
|
|
| … |
y | … | 7 | m | 14 | k | 14 | m | 7 | … |
根据表中提供的信息,有以下4 个判断:
① ![]() ;②
;② ![]() ;③ 当
;③ 当![]() 时,y 的值是 k;④
时,y 的值是 k;④ ![]() 其中判断正确的是 ( )
其中判断正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④