题目内容
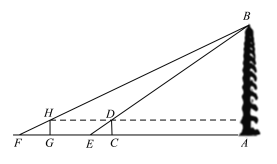
【题目】如图,正方形ABCD和正方形CEFG的边长分别为a和b,BE和DG相交于点H,连接HC,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确的结论是__________.
【答案】①②③
【解析】
由△DCG≌△BEC可证BE=DG,BE⊥DG,根据勾股定理可得BD2=DM2+BM2,EG2=ME2+MG2,则BD2+EG2=DM2+BM2+ME2+MG2,可得BD2+EG2=BG2+DE2.再把a,b代入即可证③是正确的.
如图:连接BD,EG,BE,DG的交点为M,
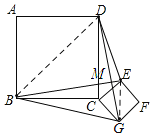
∵四边形ABCD,四边形CEFG 为正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG,
∴∠BCE=∠DCG,且BC=DC,CG=CE,
∴△BCE≌△DCG,
∴DG=BE,∠CBE=∠CDG,
∵∠DBE+∠EBC+∠BDC+∠BCD=180°,
∴∠DBE+∠EBC+∠BDC=90°,
∵∠DBE+∠CDE+∠BDC+∠BMD=180°,
∴∠DCB=∠DMB=90°,
∴BE⊥DG故①②正确;
∵BE⊥DG,
∴BD2=DM2+BM2,EG2=ME2+MG2,
∴BD2+EG2=DM2+BM2+ME2+MG2,
∴BD2+EG2=BG2+DE2,
∴AB2+AD2+EC2+CG2=BG2+DE2,
∴2a2+2b2=BG2+DE2,故③正确
故答案为:①②③.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目