题目内容
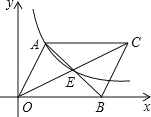
【题目】如图,在△ABC中,AD平分∠CAB,点F在边AC上,若∠CAB+∠BDF=180°.求证:DF=DB.
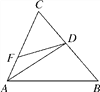
【答案】见解析.
【解析】在AB上截取AE=AF,根据角平分线和公共边得出△ADF和△ADE全等,从而得出DF=DE,根据∠CAB+∠BDF+∠5+∠B=360°,∠CAB+∠BDF=180°,得出∠5+∠B=180°,根据平角的性质以及∠5=∠3得出∠B=∠4,从而得出答案.
解:如图,在AB上截取AE=AF,∵AD平分∠CAB,∴∠1=∠2,
在△ADF和△ADE中,AF=AE,∠1=∠2,AD=AD,∴△ADF≌△ADE(SAS),
∴DF=DE,∠5=∠3,∵∠CAB+∠BDF+∠5+∠B=360°,∠CAB+∠BDF=180°,
∴∠5+∠B=180°, 又∵∠3+∠4=180°,∠5=∠3, ∴∠B=∠4,
∴DB=DE, ∴DF=DB.

练习册系列答案
相关题目