题目内容
【题目】在如图所示的直角坐标系中，解答下列问题：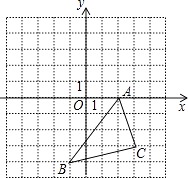 
（1）分别写出A、B两点的坐标；
（2）将△ABC绕点A顺时针旋转90°，画出旋转后的△AB1C1；
（3）求出线段B1A所在直线l的函数解析式，并写出在直线l上从B1到A的自变量x的取值范围．
【答案】
（1）解：从图中可得出：
A（2，0），B（﹣1，﹣4）
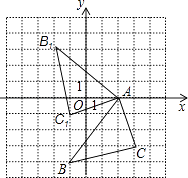
（2）解：画图
（3）解：设线段B1A所在直线l的解析式为：y=kx+b（k≠0），
∵B1（﹣2，3），A（2，0），
∴ 
，
，
∴线段B1A所在直线l的解析式为： 
，
线段B1A的自变量x的取值范围是：﹣2≤x≤2
【解析】（1）从直角坐标系中读出点的坐标．（2）让三角形的各顶点都绕点A顺时针旋转90°后得到对应点，顺次连接即可．（3）先设出一般的一次函数的解析式，再把点的坐标代入求解析式即可．
【考点精析】通过灵活运用确定一次函数的表达式，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法即可以解答此题．
练习册系列答案
阅读快车系列答案
相关题目
