题目内容
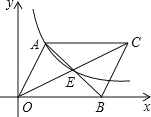
【题目】如图,平行四边形AOBC中,对角线交于点E,双曲线y=![]() (k>0)经过A、E两点, 若平行四边形AOBC的面积为30,则k=__________.
(k>0)经过A、E两点, 若平行四边形AOBC的面积为30,则k=__________.
【答案】10
【解析】如图,过A作AD⊥OB于D,EF⊥OB于F,设A(x,![]() ),B(a,0),得到EF为△ABD的中位线,可表示出EF的长,由OB-OD可得BD的长,根据F为BD的中点,得到FB的长,由OB-FB可得出OF的长,表示出E的坐标,代入反比例解析式中,得到a=3x,再由BO与AD的积为平行四边形的面积,表示出平行四边形的面积,根据平行四边形AOBC的面积为30,列出等式,将a=3x代入可得出k的值.
),B(a,0),得到EF为△ABD的中位线,可表示出EF的长,由OB-OD可得BD的长,根据F为BD的中点,得到FB的长,由OB-FB可得出OF的长,表示出E的坐标,代入反比例解析式中,得到a=3x,再由BO与AD的积为平行四边形的面积,表示出平行四边形的面积,根据平行四边形AOBC的面积为30,列出等式,将a=3x代入可得出k的值.
如图,过A作AD⊥OB于D,EF⊥OB于F,设A(x,![]() ),B(a,0),
),B(a,0),

∵四边形AOBC是平行四边形,
∴AE=EB,
∴EF为△ABD的中位线,
∴EF=![]() AD=
AD=![]() ,DF=
,DF=![]() (a-x),OF=OD+DF=
(a-x),OF=OD+DF=![]() ,
,
∴E(![]() ,
,![]() ),
),
∵E在双曲线y=![]() 上,
上,
∴![]()
![]() =k,
=k,
∴a=3x,
∵SAOBC=OBAD=30,
∴a![]() =3x
=3x![]() =3k=30,
=3k=30,
解得:k=10.
故答案为:10.

练习册系列答案
相关题目