题目内容
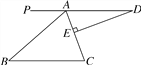
【题目】如图,等边△ABC和等边△ECD的边长相等,BC与CD两边在同一直线上,请根据如下要求,使用无刻度的直尺,通过连线的方式画图.
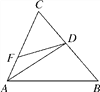
(1)在图1中画一个直角三角形; (2)在图2中画出∠ACE的平分线.
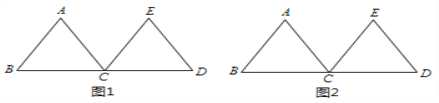
【答案】详见解析.
【解析】试题分析:(1)直接利用等边三角形的性质结合菱形的性质得出△ABD为直角三角形,同理可知,△BED也为直角三角形;
(2)利用菱形的判定与性质得出△AFG≌△EFH,得出FG=FH,进而结合角平分线的判定得出答案.
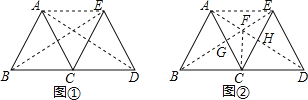
解:(1)如图①所示:连接AE,
∵△ABC与△ECD全等且为等边三角形,
∴四边形ACDE为菱形,连接AD,则AD平分∠EDC,
∴∠ADC=30°,
∵∠ABC=60°,
∴∠BAD=90°,
则△ABD为直角三角形,同理可知,△BED也为直角三角形;
(2)如图②所示:连接AE、BE、AD,则四边形ABCE和四边形ACDE为菱形,
则AC⊥BE,AD⊥CE,设BE,AD相交于F,AC交BE于点G,CE交AD于点H,
则FG⊥AC,FH⊥BC,
由(1)得:∠BEC=∠DAC,∠AEF=∠EAF,
则AF=EF,
在△AFG和△EFH中
∵∠AGF=∠FHE,
∠GFA=∠HFE,
AF=EF,
∴△AFG≌△EFH(AAS),
∴FG=FH,
由到角两边距离相等的点在角平分线上,可知,连接CF,GF为所作的角平分线.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价![]() 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元?