题目内容
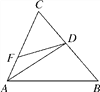
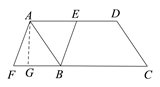
【题目】如图，在□ABCD中，E是AD的中点，延长CB到点F，使
，连接BE、AF．
（1）完成画图并证明四边形AFBE是平行四边形；
（2）若AB=6，AD=8，∠C=60°，求BE的长．
【答案】（1）见解析；（2）
【解析】（1）画图，由AE∥BF，AE=BF，可证四边形AFBE是平行四边形；（2）过点A作AG⊥BF于G ,先求BG,FG,AG，再结合勾股定理求AF，得BE＝AF.
图如下，（1）∵四边形ABCD为平行四边形，
∴AD∥BC，AD=BC，
又E是AD的中点，
，
∴AE∥BF，AE=BF，
∴四边形AFBE是平行四边形；
（2）过点A作AG⊥BF于G ,
由□ABCD可知∠ABF=∠C=60°，
又AB=6，AD=8，
∴BG＝3，FG＝1，AG＝
，
∴BE＝AF＝
.
故答案为：(1)见解析；（2）.
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
相关题目
