题目内容
【题目】甲，乙两人分别从
，
两地相向而行，甲先走3分钟后乙才开始行走，甲到达地后立即停止，乙到达地后立即以另一速度返回地，在整个行驶的过程中，两人保持各自速度匀速行走，甲，乙两人之间的距离
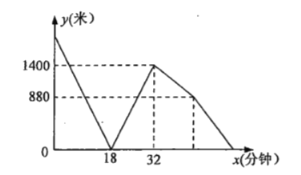
（米）与乙出发的时间
（分钟）的函数关系如图所示.当甲到达地时，则乙距离地的时间还需要________分钟.
【答案】11
【解析】
在乙出发后18分钟两车相遇，两车相遇后，又经过32-18=14分钟，两车之间的距离达到最大1400米，可以求出两车的速度和为：1400÷（32-18）=100米/分，说明此时乙车已到A地，于是可以得到：甲从开始到第一次相遇地点用时3+18=21分，而乙用14分，因此甲的速度是乙的
，根据速度和是100米/分，可求出乙车的速度为60米/分，甲车速度为40米/分；AB两地的路程为：60×32=1920米，当乙到A地时，甲距B地还有1920-1400=520米，因此甲到B地需要520÷40=13分，乙以另一速度返回13秒走的路程1920-880=1040米，所以返回速度为1040÷13=80米，到B地还要880÷80=11分．
解：两车的速度和为：1400÷（32-18）=100米/分，
甲从开始到第一次相遇地点用时3+18=21分，而乙相遇后只用14分，因此甲的速度是乙的，
甲速度为100×
=40米/分，乙的速度为100×
=60米/分，
∴AB两地的路程为：60×32=1920米，
当乙到A地时，甲距B地还有1920-1400=520米，
因此甲到B地需要520÷40=13分，
乙以另一速度返回13秒走的路程1920-880=1040米，
所以返回速度为1040÷13=80米，
到B地还要880÷80=11分．
故答案为：11
【题目】设函数y=k1x+
，且k1k2≠0，自变量x与函数值y满足以下表格：
x | …… | -4 | -3 | -2 | -1 | - |
| 1 | 2 | 3 | 4 | …… |
y | …… | -3 | -2 | -1 | 0 | 1 | -1 | 0 | 1 | m | n | …… |
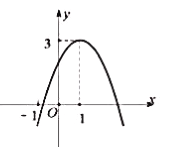
（1）根据表格直接写出y与x的函数表达式及自变量x的取值范围______
（2）补全上面表格：m=______，n=______；在如图所示的平面直角坐标系中，请根据表格中的数据补全y关于x的函数图象；
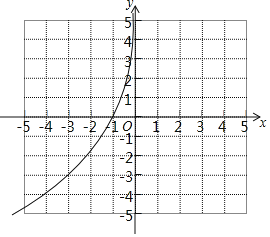
（3）结合函数图象，解决下列问题：
①写出函数y的一条性质：______；
②当函数值y≥
时，x的取值范围是______；
③当函数值y=-x时，结合图象请估算x的值为______（结果保留一位小数）
