题目内容
【题目】设函数y=k1x+![]() ,且k1k2≠0,自变量x与函数值y满足以下表格:
,且k1k2≠0,自变量x与函数值y满足以下表格:
x | …… | -4 | -3 | -2 | -1 | - |
| 1 | 2 | 3 | 4 | …… |
y | …… | -3 | -2 | -1 | 0 | 1 | -1 | 0 | 1 | m | n | …… |
(1)根据表格直接写出y与x的函数表达式及自变量x的取值范围______
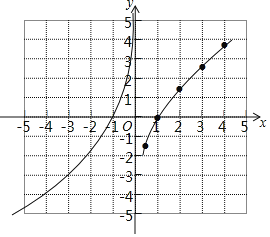
(2)补全上面表格:m=______,n=______;在如图所示的平面直角坐标系中,请根据表格中的数据补全y关于x的函数图象;
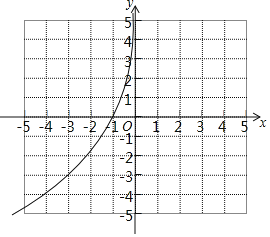
(3)结合函数图象,解决下列问题:
①写出函数y的一条性质:______;
②当函数值y≥![]() 时,x的取值范围是______;
时,x的取值范围是______;
③当函数值y=-x时,结合图象请估算x的值为______(结果保留一位小数)
【答案】(1)y=x-![]() (x≠0);(2)2
(x≠0);(2)2![]() ,3
,3![]() ;(3)①当x≥1时,y随x的增大而增大;②x=-
;(3)①当x≥1时,y随x的增大而增大;②x=-![]() 或x≥2;③±0.7
或x≥2;③±0.7
【解析】
(1)把(-1,0),(2,1![]() )代入y=k1x+
)代入y=k1x+![]() 解方程组即可得到结论;
解方程组即可得到结论;
(2)当x=3时,当x=4时,定义函数解析式即可得到结论;补全y关于x的函数图象即可;
(3)根据函数图象即可得到结论.
解:(1)把(-1,0),(2,1![]() )代入y=k1x+
)代入y=k1x+![]() 得,
得,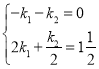 ,
,
解得: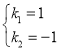 ,
,
∴y与x的函数表达式为:y=x-![]() (x≠0);
(x≠0);
故答案为:y=x-![]() (x≠0);
(x≠0);
(2)当x=3时,m=3-![]() =2
=2![]() ,当x=4时,n=4-
,当x=4时,n=4-![]() =3
=3![]() ;补全y关于x的函数图象如图所示;
;补全y关于x的函数图象如图所示;
故答案为:2![]() ,3
,3![]() ;
;
(3)由图象知,①当x≥1时,y随x的增大而增大;
②当函数值y≥![]() 时,x的取值范围是:x=-
时,x的取值范围是:x=-![]() 或x≥2;
或x≥2;
③当函数值y=-x时,结合图象请估算x的值为±0.7,
故答案为:当x≥1时,y随x的增大而增大;x=-![]() 或x≥2;±0.7.
或x≥2;±0.7.

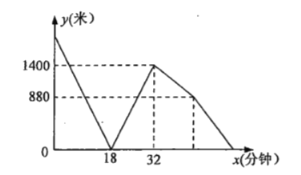
【题目】东坡商贸公司购进某种水果成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价P(元/kg)与时间t(天)之间的函数关系式P=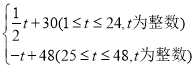 且其日销售量y(kg)与时间t(天)的关系如表下:
且其日销售量y(kg)与时间t(天)的关系如表下:
时间t(天) | 1 | 3 | 6 | 10 | 20 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | … |
(1)已知y与t之间的变化符合一次函数关系,试求在第30天的日销售量.
(2)哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,该公司决定每销售1kg水果就捐赠n元利润(0<n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.