Question

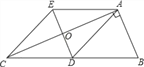
【题目】如图，在Rt△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连结EC．

（1）求证：AD=EC；

（2）求证：四边形ADCE是菱形；

（3）若AB=AO，求的值．

Answer 1

【答案】（1）证明见解析;（2）见解析;（3）．

【解析】分析：（1）先判定四边形ABDE为平行四边形，再判定四边形ADCE为平行四边形，即可得出AD=EC；
（2）根据四边形ADCE为平行四边形，且AD=CD，即可得出平行四边形ADCE为菱形；
（3）先判定OD为△ABC的中位线，得出再根据AB=AO，得出即可．

详解：(1)证明：∵AE∥BC,DE∥AB，

∴四边形ABDE为平行四边形，

∴AE=BD，

∵在Rt△ABC中，AD是斜边BC上的中线，

∴AD=CD=BD，

∴AE=CD，

又∵AE∥CD，

∴四边形ADCE为平行四边形，

∴AD=EC；

(2)由(1)可知，四边形ADCE为平行四边形，且AD=CD，

∴平行四边形ADCE为菱形；

(3)∵四边形ADCE为平行四边形，

∴AC与ED互相平分，

∴点O为AC的中点，

∵AD是边BC上的中线，

∴点D为BC边中点，

∴OD为△ABC的中位线，

∴

∵AB=AO，

∴

即的值为.