题目内容
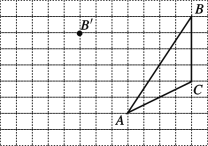
【题目】在平面直角坐标系中,A(a,0),B(0,b),a,b满足![]() =0,C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
=0,C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)求∠OAB的度数
(2)当点P运动时,PE的长是否变化?若变化,请说明理由;若不变,请求PE的长
(3)若∠OPD=45度,求点D的坐标

【答案】(1)45°;(2)3;(3)(![]() ,0)
,0)
【解析】分析:(1)根据非负数的性质即可求得a、b的值,从而得到△AOB是等腰直角三角形,据此可求;
(2)根据等腰直角三角形的性质以及三角形的外角的性质可以得到∠POC=∠DPE,即可得证△POC≌△DPE,则OC=PE,OC的长度可根据等腰直角三角形的性质可求;
(3)利用等腰三角形的性质,以及外角的性质,证得∠POC=∠DPE,即可得到△POC≌△DPE,根据全等三角形的对应边相等,即可求得OD的长,从而求得D的坐标.
详解:(1)根据题意得:a=b,a-3=0.解得:a=b=3,∴OA=OB
又∵∠AOB=90°,∴△AOB是等腰直角三角形,∠OAB=45°。
(2)PE值不变。
理由:∵△AOB是等腰直角三角形,且AC=BC, ∴∠AOC=∠BOC=45°,
又因OC垂直AB于C,故PO=PD,∴∠POD=∠PDO. 又因∠POD=45°+∠POC,
∠POD=45°+∠DPE∴∠POC=∠DPE。
∴在△POC和△DPE中,
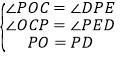
∴△POC≌△DPE. ∴OC=PE
又因OC=![]() AB=3, ∴PE=3
AB=3, ∴PE=3
(3)∵PO=PD, ∴∠POD=∠PDO=![]() =67.5°
=67.5°
∴∠PDA=180°-∠PDO=180°-67.5°=112.5°
∵∠POD=∠A+∠APD,
∴∠APD=67.5°-45°=22.5°, ∴∠BPO=180°-∠OPD-∠APD=112.5°
∴∠PDA=∠BPO
∴在△POB和△DPA中,
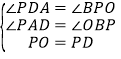
∴△POB≌△DPA(AAS)
PA=OB= 3![]() , ,DA=PB= 6-3
, ,DA=PB= 6-3![]()
∴ OD=OA-DA=3![]() -(6-3
-(6-3![]() )=6
)=6![]() -6
-6
∴ D(6![]() -6,0)
-6,0)

【题目】为了庆祝即将到来的“五四”青年节,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩80≤x<100范围内的学生有多少人?